2019-09-08

yukicoder No.878 Range High-Element Query

解法

マージソートの過程をセグ木に保存する方法(蟻本 p171)と同じ要領で，各頂点にその区間に対応する「高い要素」の列を保存しておく．左の子と右の子の2つの列をmergeするときには，左の子の列はそのままで，右の子の列の要素のうち左の子の列の最大の頂点より大きい「高い要素」を順番に追加すればよい．区間 $[a,b)$ の $x$ より大きく「高い要素」の個数と最大の要素を求められればこのmergeは行うことができる．merge結果 = (左の子の列の「高い要素」の個数) + (右の子の列の要素のうち，左の子の列の最大の要素より大きい「高い要素」の個数) とすればよい．各クエリについて答えは seg.query(l, r+1, -LLINF) となる．

#include <bits/stdc++.h>

using namespace std;
using ll = long long;
// #define int ll
using PII = pair<ll, ll>;

#define FOR(i, a, n) for (ll i = (ll)a; i < (ll)n; ++i)
#define REP(i, n) FOR(i, 0, n)
#define ALL(x) x.begin(), x.end()

template<typename T> T &chmin(T &a, const T &b) { return a = min(a, b); }
template<typename T> T &chmax(T &a, const T &b) { return a = max(a, b); }
template<typename T> bool IN(T a, T b, T x) { return a<=x&&x<b; }
template<typename T> T ceil(T a, T b) { return a/b + !!(a%b); }

template<typename T> vector<T> make_v(size_t a) { return vector<T>(a); }
template<typename T,typename... Ts>
auto make_v(size_t a,Ts... ts) {
    return vector<decltype(make_v<T>(ts...))>(a,make_v<T>(ts...));
}
template<typename T,typename V> typename enable_if<is_class<T>::value==0>::type
fill_v(T &t, const V &v) { t=v; }
template<typename T,typename V> typename enable_if<is_class<T>::value!=0>::type
fill_v(T &t, const V &v ) { for(auto &e:t) fill_v(e,v); }

template<class S,class T>
ostream &operator <<(ostream& out,const pair<S,T>& a) {
    out<<'('<<a.first<<','<<a.second<<')'; return out;
}
template<class T>
ostream &operator <<(ostream& out,const vector<T>& a){
    out<<'[';
    for(const T &i: a) out<<i<<',';
    out<<']';
    return out;
}
template<class T>
ostream &operator <<(ostream& out, const set<T>& a) {
    out<<'{';
    for(const T &i: a) out<<i<<',';
    out<<'}';
    return out;
}
template<class T, class S>
ostream &operator <<(ostream& out, const map<T,S>& a) {
    out<<'{';
    for(auto &i: a) out<<i<<',';
    out<<'}';
    return out;
}

int dx[] = {0, 1, 0, -1}, dy[] = {1, 0, -1, 0}; // DRUL
const int INF = 1<<30;
const ll LLINF = 1LL<<60;
const ll MOD = 1000000007;

struct segTreeRangeFreq {
    int n;
    vector<vector<ll>> dat;
    // 初期化 O(NlogN)
    segTreeRangeFreq() {}
    segTreeRangeFreq(vector<vector<ll>> v) {
        n = 1; while(n < (ll)v.size()) n *= 2;
        dat.resize(2*n-1);
        REP(i, v.size()) {
            dat[i+n-1] = v[i];
        }
        for(int i=n-2; i>=0; --i) {
            dat[i].resize(dat[i*2+1].size());
            REP(j, dat[i*2+1].size()) dat[i][j] = dat[i*2+1][j];
            FOR(j, (ll)dat[i*2+1].size(), (ll)dat[i*2+1].size()+(ll)dat[i*2+2].size()) {
                if(dat[i*2+2][j-dat[i*2+1].size()] > dat[i].back()) {
                    dat[i].push_back(dat[i*2+2][j-dat[i*2+1].size()]);
                }
            }
        }
    }
    // [a, b) のxより大きい高い要素の個数とmax
    PII query(int a, int b, ll x, int k, int l, int r) {
        if(b <= l || r <= a) return PII(0, x);
        if(a <= l && r <= b) {
            ll itr = upper_bound(ALL(dat[k]), x) - dat[k].begin();
            return PII((ll)dat[k].size()-itr, dat[k].size()?max(x, dat[k].back()):x);
        }
        PII vl = query(a, b, x, k*2+1, l, (l+r)/2);
        PII vr = query(a, b, vl.second, k*2+2, (l+r)/2, r);
        return PII(vl.first + vr.first, max({x, vl.second, vr.second}));
    }
    PII query(int a, int b, ll x) { return query(a, b, x, 0, 0, n); }
};

signed main(void)
{
    cin.tie(0);
    ios::sync_with_stdio(false);

    ll n, q;
    cin >> n >> q;
    vector<ll> a(n);
    REP(i, n) cin >> a[i];

    vector<vector<ll>> v(n,vector<ll>(1));
    REP(i, n) v[i][0] = a[i];
    segTreeRangeFreq seg(v);

    while(q--) {
        ll t, l, r;
        cin >> t >> l >> r;
        l--, r--;
        cout << seg.query(l, r+1, -LLINF).first << endl;
    }

    return 0;
}

2019-09-08

yukicoder No.877 Range ReLU Query

競技プログラミング yukicoder

問題ページ

解法

区間 $[l, r$ ]に $x$ より大きい要素しかないのであれば $\sum_{i=l}^{r} a_i - (r-l+1)x$ を計算すればよい．逆に $x$ 以下の要素しかなければ0を出力するだけである．区間 $[l,r$ ]の和， $x$ 以下の要素の個数， $x$ 以下の要素の和が求まれば $x$ より大きい要素と $x$ 以下の要素に場合分けしてそれぞれ計算すればよい．
普通の区間和は累積和を取っておけば高速に求められる．ある区間の $x$ 以下の要素について扱いたいときに更新がないのであれば，マージソートの過程をセグメント木に保存しておけばよい(蟻本 p171)．最初にセグ木を構築するときに累積和を取っておくことで， $x$ 以下の要素の和を求めることはできる．
したがって $O(N(\log N)^2)$ で解けた．

#include <bits/stdc++.h>

using namespace std;
using ll = long long;
// #define int ll
using PII = pair<ll, ll>;

#define FOR(i, a, n) for (ll i = (ll)a; i < (ll)n; ++i)
#define REP(i, n) FOR(i, 0, n)
#define ALL(x) x.begin(), x.end()

template<typename T> T &chmin(T &a, const T &b) { return a = min(a, b); }
template<typename T> T &chmax(T &a, const T &b) { return a = max(a, b); }
template<typename T> bool IN(T a, T b, T x) { return a<=x&&x<b; }
template<typename T> T ceil(T a, T b) { return a/b + !!(a%b); }

template<typename T> vector<T> make_v(size_t a) { return vector<T>(a); }
template<typename T,typename... Ts>
auto make_v(size_t a,Ts... ts) {
    return vector<decltype(make_v<T>(ts...))>(a,make_v<T>(ts...));
}
template<typename T,typename V> typename enable_if<is_class<T>::value==0>::type
fill_v(T &t, const V &v) { t=v; }
template<typename T,typename V> typename enable_if<is_class<T>::value!=0>::type
fill_v(T &t, const V &v ) { for(auto &e:t) fill_v(e,v); }

template<class S,class T>
ostream &operator <<(ostream& out,const pair<S,T>& a) {
    out<<'('<<a.first<<','<<a.second<<')'; return out;
}
template<class T>
ostream &operator <<(ostream& out,const vector<T>& a){
    out<<'[';
    for(const T &i: a) out<<i<<',';
    out<<']';
    return out;
}
template<class T>
ostream &operator <<(ostream& out, const set<T>& a) {
    out<<'{';
    for(const T &i: a) out<<i<<',';
    out<<'}';
    return out;
}
template<class T, class S>
ostream &operator <<(ostream& out, const map<T,S>& a) {
    out<<'{';
    for(auto &i: a) out<<i<<',';
    out<<'}';
    return out;
}

int dx[] = {0, 1, 0, -1}, dy[] = {1, 0, -1, 0}; // DRUL
const int INF = 1<<30;
const ll LLINF = 1LL<<60;
const ll MOD = 1000000007;

struct segTreeRangeFreq {
    int n;
    vector<vector<ll>> dat;
    vector<vector<ll>> rui;
    // 初期化 O(NlogN)
    segTreeRangeFreq() {}
    segTreeRangeFreq(vector<vector<ll>> v) {
        n = 1; while(n < (ll)v.size()) n *= 2;
        dat.resize(2*n-1);
        rui.resize(2*n-1);
        REP(i, v.size()) {
            dat[i+n-1] = rui[i+n-1] = v[i];
        }
        for(int i=n-2; i>=0; --i) {
            dat[i].resize(dat[i*2+1].size() + dat[i*2+2].size());
            merge(ALL(dat[i*2+1]), ALL(dat[i*2+2]), dat[i].begin());
            if(dat[i].size() == 0) continue;
            rui[i].resize(dat[i].size());
            rui[i][0] = dat[i][0];
            FOR(j, 1, rui[i].size()) {
                rui[i][j] = rui[i][j-1] + dat[i][j];
            }
        }
    }
    // [a, b) のx以下の要素の和を返す O(log^2N)
    PII query(int a, int b, ll x, int k, int l, int r) {
        if(b <= l || r <= a) return PII(0, 0);
        if(a <= l && r <= b) {
            ll itr = upper_bound(ALL(dat[k]), x) - dat[k].begin();
            return PII(itr, itr-1<0?0:rui[k][itr-1]);
        }
        PII vl = query(a, b, x, k*2+1, l, (l+r)/2);
        PII vr = query(a, b, x, k*2+2, (l+r)/2, r);
        return PII({vl.first+vr.first, vl.second+vr.second});
    }
    PII query(int a, int b, ll x) { return query(a, b, x, 0, 0, n); }
};

signed main(void)
{
    cin.tie(0);
    ios::sync_with_stdio(false);

    ll n, q;
    cin >> n >> q;
    vector<ll> a(n);
    REP(i, n) cin >> a[i];

    vector<vector<ll>> v(n, vector<ll>(1));
    REP(i, n) v[i][0] = a[i];
    segTreeRangeFreq seg(v);
    FOR(i, 1, n) a[i] += a[i-1];

    while(q--) {
        ll t, l, r, x;
        cin >> t >> l >> r >> x;
        l--, r--;

        ll ret = a[r] - (l==0?0:a[l-1]);
        PII val = seg.query(l, r+1, x);
        ret -= val.second;
        ret -= (r-l+1-val.first) * x;
        cout << ret << endl;
    }

    return 0;
}

2019-09-04

CODE FESTIVAL 2016 Grand Final J - 123 Pairs

競技プログラミング AtCoder

問題ページ

解法

ペアとなっている2要素を区間として，区間が交差しない部分は独立に考えてよさそう．各区間でどのようなペアのとり方が存在するのか考えると以下のパターンしかない．

(1) 1
(2) 2 3 … 3 2
(3) 3 1
(4) 3 3 3

f:id:ferin_tech:20190904155032j:plain

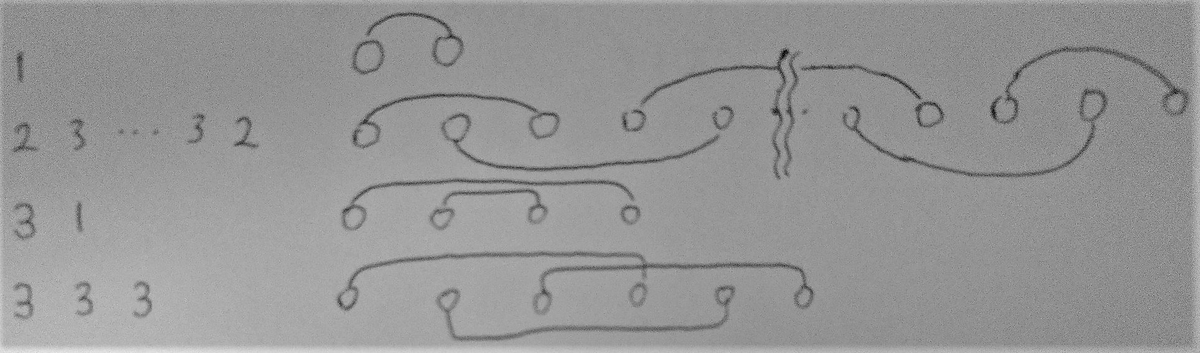
2は(2)以外で使用できないので(2)はB/2個となる．(1)をw個とすると(3)はA-w個となる．(4)をz個とすると，(2)の間に使用する3は合計でC-(A-w)-3z個となる．
まとめると(1)をw個，(2)をB/2個，(3)をA-w個，(4)をz個，(2)の間に使用する3がC-(A-w)-3z個となる．(2)の間に使用する3についてはC-(A-w)-3z個をB/2個に分割するので $\binom{C-(A-w)-3z+B/2-1}{B/2-1}$ 通りとなる．(1)～(4)を配置する方法は (w+B/2+A-w+z)!/(w!(B/2)!(A-w)!z!) 通りとなる．あとはw,zをO(N^2)通り全探索すればよい．

#include <bits/stdc++.h>

using namespace std;
using ll = long long;
// #define int ll
using PII = pair<ll, ll>;

#define FOR(i, a, n) for (ll i = (ll)a; i < (ll)n; ++i)
#define REP(i, n) FOR(i, 0, n)
#define ALL(x) x.begin(), x.end()

template<typename T> T &chmin(T &a, const T &b) { return a = min(a, b); }
template<typename T> T &chmax(T &a, const T &b) { return a = max(a, b); }
template<typename T> bool IN(T a, T b, T x) { return a<=x&&x<b; }
template<typename T> T ceil(T a, T b) { return a/b + !!(a%b); }

template<typename T> vector<T> make_v(size_t a) { return vector<T>(a); }
template<typename T,typename... Ts>
auto make_v(size_t a,Ts... ts) {
    return vector<decltype(make_v<T>(ts...))>(a,make_v<T>(ts...));
}
template<typename T,typename V> typename enable_if<is_class<T>::value==0>::type
fill_v(T &t, const V &v) { t=v; }
template<typename T,typename V> typename enable_if<is_class<T>::value!=0>::type
fill_v(T &t, const V &v ) { for(auto &e:t) fill_v(e,v); }

template<class S,class T>
ostream &operator <<(ostream& out,const pair<S,T>& a) {
    out<<'('<<a.first<<','<<a.second<<')'; return out;
}
template<class T>
ostream &operator <<(ostream& out,const vector<T>& a){
    out<<'[';
    for(const T &i: a) out<<i<<',';
    out<<']';
    return out;
}
template<class T>
ostream &operator <<(ostream& out, const set<T>& a) {
    out<<'{';
    for(const T &i: a) out<<i<<',';
    out<<'}';
    return out;
}
template<class T, class S>
ostream &operator <<(ostream& out, const map<T,S>& a) {
    out<<'{';
    for(auto &i: a) out<<i<<',';
    out<<'}';
    return out;
}

int dx[] = {0, 1, 0, -1}, dy[] = {1, 0, -1, 0}; // DRUL
const int INF = 1<<30;
const ll LLINF = 1LL<<60;
const ll MOD = 1000000007;

template<ll MOD>
struct modint {
    ll x;
    modint(): x(0) {}
    modint(ll y) : x(y>=0 ? y%MOD : y%MOD+MOD) {}
    static constexpr ll mod() { return MOD; }
    // e乗
    modint pow(ll e) {
        ll a = 1, p = x;
        while(e > 0) {
            if(e%2 == 0) {p = (p*p) % MOD; e /= 2;}
            else {a = (a*p) % MOD; e--;}
        }
        return modint(a);
    }
    modint inv() const {
        ll a=x, b=MOD, u=1, y=1, v=0, z=0;
        while(a) {
            ll q = b/a;
            swap(z -= q*u, u);
            swap(y -= q*v, v);
            swap(b -= q*a, a);
        }
        return z;
    }
    // Comparators
    bool operator <(modint b) { return x < b.x; }
    bool operator >(modint b) { return x > b.x; }
    bool operator<=(modint b) { return x <= b.x; }
    bool operator>=(modint b) { return x >= b.x; }
    bool operator!=(modint b) { return x != b.x; }
    bool operator==(modint b) { return x == b.x; }
    // Basic Operations
    modint operator+(modint r) const { return modint(*this) += r; }
    modint operator-(modint r) const { return modint(*this) -= r; }
    modint operator*(modint r) const { return modint(*this) *= r; }
    modint operator/(modint r) const { return modint(*this) /= r; }
    modint &operator+=(modint r) {
        if((x += r.x) >= MOD) x -= MOD;
        return *this;
    }
    modint &operator-=(modint r) {
        if((x -= r.x) < 0) x += MOD;
        return *this;
    }
    modint &operator*=(modint r) {
    #if !defined(_WIN32) || defined(_WIN64)
        x = x * r.x % MOD; return *this;
    #endif
        unsigned long long y = x * r.x;
        unsigned xh = (unsigned) (y >> 32), xl = (unsigned) y, d, m;
        asm(
            "divl %4; \n\t"
            : "=a" (d), "=d" (m)
            : "d" (xh), "a" (xl), "r" (MOD)
        );
        x = m;
        return *this;
    }
    modint &operator/=(modint r) { return *this *= r.inv(); }
    // increment, decrement
    modint operator++() { x++; return *this; }
    modint operator++(signed) { modint t = *this; x++; return t; }
    modint operator--() { x--; return *this; }
    modint operator--(signed) { modint t = *this; x--; return t; }

    template<class T>
    friend modint operator*(T l, modint r) { return modint(l) *= r; }
    template<class T>
    friend modint operator+(T l, modint r) { return modint(l) += r; }
    template<class T>
    friend modint operator-(T l, modint r) { return modint(l) -= r; }
    template<class T>
    friend modint operator/(T l, modint r) { return modint(l) /= r; }
    template<class T>
    friend bool operator==(T l, modint r) { return modint(l) == r; }
    template<class T>
    friend bool operator!=(T l, modint r) { return modint(l) != r; }
    // Input/Output
    friend ostream &operator<<(ostream& os, modint a) { return os << a.x; }
    friend istream &operator>>(istream& is, modint &a) { return is >> a.x; }
    friend string to_frac(modint v) {
        static map<ll, PII> mp;
        if(mp.empty()) {
            mp[0] = mp[MOD] = {0, 1};
            FOR(i, 2, 1001) FOR(j, 1, i) if(__gcd(i, j) == 1) {
                mp[(modint(i) / j).x] = {i, j};
            }
        }
        auto itr = mp.lower_bound(v.x);
        if(itr != mp.begin() && v.x - prev(itr)->first < itr->first - v.x) --itr;
        string ret = to_string(itr->second.first + itr->second.second * ((int)v.x - itr->first));
        if(itr->second.second > 1) {
            ret += '/';
            ret += to_string(itr->second.second);
        }
        return ret;
    }
};
using mint = modint<1000000007>;

// 前計算O(N) クエリO(1)
mint combi(ll N, ll K) {
    const int maxN=5e5; // !!!
    static mint fact[maxN+1]={},factr[maxN+1]={};
    if (fact[0]==0) {
        fact[0] = factr[0] = 1;
        FOR(i, 1, maxN+1) fact[i] = fact[i-1] * i;
        factr[maxN] = fact[maxN].inv();
        for(ll i=maxN-1; i>=0; --i) factr[i] = factr[i+1] * (i+1);
    }
    if(K<0 || K>N) return 0; // !!!
    return factr[K]*fact[N]*factr[N-K];
}

mint frac[20001], ifrac[20001];
signed main(void)
{
    cin.tie(0);
    ios::sync_with_stdio(false);

    ll n, a, b, c;
    cin >> n >> a >> b >> c;

    if(b%2) {
        cout << 0 << endl;
        return 0;
    }

    frac[0] = 1;
    FOR(i, 1, 20001) frac[i] = frac[i-1] * i;
    ifrac[20000] = frac[20000].inv();
    for(ll i=19999; i>=0; --i) ifrac[i] = ifrac[i+1] * (i+1);

    if(b == 0) {
        mint ret = 0;
        REP(w, a+1) {
            ll x = a-w, z = (c-x)/3;
            if(c-x<0 || (c-x)%3 != 0) continue;
            mint add = frac[w+x+z] * ifrac[w] * ifrac[x] * ifrac[z];
            ret += add;
        }
        cout << ret << endl;
        return 0;
    }

    mint ret = 0;
    REP(w, a+1) REP(z, c/3+1) {
        ll x = a-w, y = b/2, rest = c-x-3*z;
        if(x+3*z > c) continue;
        mint add = frac[w+x+y+z] * ifrac[w] * ifrac[x] * ifrac[y] * ifrac[z] * combi(rest+y-1, y-1);
        ret += add;
    }
    cout << ret << endl;

    return 0;
}

2019-09-02

TTPC2019参加記

競技プログラミング

コンテスト

東京工業大学プログラミングコンテスト2019 - AtCoder
チームolphe_konaiphe(oshibori，tsutaj，ferin)で参加しました．

B問題

部分文字列okyoのあとに部分文字列echが存在するかを判定すればいいことがわかったので書いてAC

A問題

oshiboriさんが解いてた．

D問題

tsutajさんに素数=素数+素数となる場合，片方の素数は必ず2と教えてもらった．あとはgrundy数を愚直に計算するだけなので書いて出した．

C問題

tsutajさんに方針の確認だけされたのでokだと思うと答えたら通ってた．

E問題

「同じ行/列の要素をswapしても行/列の和には影響しないのでswapをしてうまいこと和をずらすみたいなことを考えると奇数の場合は構成できる．偶数の場合 $1+2+\ldots+N^2$ と $0+1+2+\ldots+N-1$ が $N$ を法として合同になることはないので必ずNoになる．」みたいな考察をtsutajさんとしたので書いてもらうと通る．

F問題

DAGしか与えられないことを教えてもらう．始点と終点が1つずつならDPするだけ．2つあって合流したり分岐したりするのが複雑そうなのでDPっぽい． $dp \lbrack$ 頂点 $v \rbrack \lbrack w$ から連結 $/y$ から連結 $/w$ と $y$ 両方から連結 $\rbrack =$ 連結するのに必要な最小コストとするDPができそう．これだけだと分岐した後を表現できないが，分岐したあとなら独立に解けるので終点からの最短距離を求めておけばいいとtsutajさんに教えてもらう．合流せずにwからx，yからzにそれぞれ独立に向かうパターンを忘れていてWAを生やすがなんとかAC．

G問題

Kが大きい場合はどうせ $26^{N/2}$ になるとか，気合で詰めれば解けそうな見た目をしているとかtsutajさんと話す．

H問題

oshiboriさんに平衡二分探索木があれば解けると言われ，さすがにそんなライブラリ使わないのでは？と思ったけど他の方法が全く思い浮かばない．実装がやばそうなのでとりあえず放置．

O問題

$2^{11}=2048$ なので3マスで2倍を表現して2べきを頑張るみたいないつものだろと思い，考えたが思いつかないので放置．

H問題

実装に入れる問題がHしかない．仕方がないのでRBSTを貼って頑張ることにする．
クエリを前から見ていく．そもそも連結な集合を結ぶ場合答えは変化しないのでどうでもいい．新たに連結した集合以外の頂点の部分が変化することはないので，新たに連結した集合に関してのみ解ければよい．頂点の連結性についてはUnionFind等を使えば管理できる．
pが大きい方から並べる順序付き集合とxの和を各連結成分に持たせる．pが大きい方から貪欲に割り当てて行けばよいので，集合のprefixのxやpxの和が取得できれば連結成分ごとに答えを求めることは可能．集合のマージはマージテクで高速にできる．
気合で実装をするとサンプルが合ったので通る気しない～～～と言いながら投げたら通った✌🏻．

G問題

i文字目と対称の位置にある文字が同じ/違うものが何個あるかと文字列の中心が存在するか(=奇数長か)で3グループに分ける．各グループに操作する回数を何回割り振るか？で元の文字列が何通りあり得るかが変わってくる．それぞれのグループで何通りあるか計算した後，畳み込みを計算すれば答えが求められそう．という話をtsutajさんから聞く．任意MODのNTTが想定解ではないだろうなあと話し合いつつも考察は合っていると思うので書いてもらう．

M問題

Gの実装をチームメンバーの二人に任せて，割と解かれていたMをやることにする．まず木の根を一つに固定した場合はdfsすれば解けることがわかる．各頂点を根にした場合を求めたいので明らかに全方位木DPっぽさがある．全方位木DPで親側の情報として渡すものは，(親側の部分木の転倒数)+(新たに根になる頂点より小さい頂点の数)となる．これを求めるには各頂点を根とした部分木で転倒数と自分より小さい頂点が何個あるか？をそれぞれ計算できればよい．順序付き集合をマージしていきながらdfsを1回すればこの値は計算できるので，全方位木DPで解ける．Gと交代しながら実装するとサンプルが合ったので投げると通る．

G問題

Nが偶数のとき1ケース，奇数のとき数ケースが通らないということで考えるが間違っている場所がわからない．色々試して調整するものの合わずコンテスト終了．

後半集中が切れててGのK=0のコーナーを指摘できなかったのとO問題にもうちょっと時間を割けばよかったかな～というのが反省点．

懇親会では寿司とピザがフューチャーさんから提供された(ありがとうございます🙏)ので食べながらお話したりした．翌日にはリアル脱出ゲームに行ったりボドゲをやったり夕飯を食べたりした．周りの謎解きスキルが高くて脱出のプロだった．

2019-08-11

ラグランジュ補間

競技プログラミング

次の問題を解くアルゴリズム
$n$ 次以下の多項式 $f$ が存在する． $f(x_i) = y_i$ となる $(x_i, y_i)$ の組が $n+1$ 個存在するときに $f$ を復元しろ．

求める $f$ の形式で場合分けする．

$f(T)$ を一つ求める ( $T$ はgiven)

$f_i(x) = \prod_{j \neq i} (x-x_j) = \prod_{j} (x-x_j) / (x-x_i)$ とすると $f(x) = \sum_{i=0}^n c_i f_i(x)$ (ただし $c_i$ は未知の係数) と書ける．このように $f_i(x)$ を定めると $f_i(x_j) = 0\ \ (i \neq j)$ となるのが都合がいい． $f(x_i) = c_i f_i(x_i)$ となるため $c_i = f(x_i) / f_i(x_i)$ と係数 $c_i$ を求められる．
$f_i(x_i)$ は $O(n)$ で求められるので $O(n^2)$ で $c_i\ \ (0 \le i \le n)$ を求められる．

$f_i(T)$ は $O(n)$ で求められるので $f(T) = c_0 f_0(T) + c_1 f_1(T) + \ldots + c_n f_n(T)$ は $O(n^2)$ で求められる．

// x座標が相異なるn+1点(x_i,y_i)を通るn次以下の多項式f(T)の値を返す
// O(n^2)
mint lagrange_interpolation(vector<mint> x, vector<mint> y, mint T) {
    const ll n = x.size() - 1;
    mint ret = 0;
    REP(i, n+1) {
        mint t = 1;
        REP(j, n+1) {
            if(i == j) continue;
            t *= T-x[j];
            t /= x[i]-x[j];
        }
        ret += t * y[i];
    }
    return ret;
}

ARC033 D - 見たことのない多項式の部分点「提出」

$f(x)$ の係数を求める

$c_i$ を求めるところまでは同じようにやる．

$f(x) = \sum_{i=0}^n c_i f_i(x)$ を求めるために $f_i(x)$ を $O(n)$ で求める．これを戻すDPを使って行う． $(x-x_0)(x-x_1)\cdots(x-x_n)$ の $x^j$ の係数をDPを使って計算する． $dp(i,j) = (x-a_i$ まで見たときの $x^j$ の係数 $)$ とする．遷移は $dp(i,j) = dp(i-1,j) \times -x_i + dp(i-1,j-1)$ となる．このDPの計算は $O(n^2)$ でできる．

$dp(i,j)$ から $dp(i-1,j)$ を復元することを考える． $j$ が小さい方から順番に見ていく． $dp(i,0) = dp(i-1,0) \times -x_i$ であるから $dp(i-1,0) = -dp(i,0) / x_i$ と求められる． $dp(i,j) = dp(i-1,j)\times -x_i + dp(i-1,j-1)$ であるから $dp(i-1,j) = -(dp(i,j)-dp(i-1,j-1))/x_i$ と求められる．このようにdpを戻す操作は $(x-x_0)(x-x_1)\cdots(x-x_n)$ を $(x-x_i)$ で割る操作に対応する．

よって $f_i(x)$ を $O(n)$ で求めることができたので $f(x) = \sum_{i=0}^n c_i f_i(x)$ を $O(n^2)$ で求められた．

// x座標が相異なるn+1点(x_i,y_i)を通るn次以下の多項式f(x)を返す
// O(n^2)
vector<mint> lagrange_interpolation(vector<mint> x, vector<mint> y) {
    const ll n = x.size() - 1;
    REP(i, n+1) {
        mint t = 1;
        REP(j, n+1) if(i != j) t *= x[i]-x[j];
        y[i] /= t;
    }
    ll cur = 0, nxt = 1;
    vector<vector<mint>> dp(2, vector<mint>(n+2));
    dp[0][0] = -1 * x[0], dp[0][1] = 1;
    FOR(i, 1, n+1) {
        REP(j, n+2) {
            dp[nxt][j] = dp[cur][j] * -1 * x[i];
            if(j >= 1) dp[nxt][j] += dp[cur][j-1];
        }
        swap(nxt, cur);
    }
    vector<mint> xinv(n+1);
    REP(i, n+1) xinv[i] = x[i].inv();
    vector<mint> ret(n+1);  // f(x)
    REP(i, n+1) {
        if(y[i]==0) continue;
        // 0割り対策の場合分け
        if(x[i] == 0) {
            REP(j, n+1) ret[j] += dp[cur][j+1] * y[i];
        } else {
            ret[0] -= dp[cur][0] * xinv[i] * y[i];
            mint pre = -1 * dp[cur][0] * xinv[i];
            FOR(j, 1, n+1) {
                ret[j] -= (dp[cur][j] - pre) * xinv[i] * y[i];
                pre = -1 * (dp[cur][j] - pre) * xinv[i];
            }
        }
    }
    return ret;
}

ABC137 F - Polynomial Construction 「提出」

与えられる点の座標が等差数列

$x_i$ が等差数列になってるケースではもっと高速に解ける．
初項 $a$ で交差 $d$ の等差数列とする．

$f(T)$ を一つ求める (Tはgiven)

求めるのに $O(n^2)$ かけていた $f_i(x_i), f_i(T)$ を高速に求めることができればうれしい．

$f_i(x_i)$ と $f_{i+1}(x_{i+1})$ の形が似ていることを使う．
$f_i(x_i) = (x_i-x_0)\times(x_i-x_1)\times\cdots\times d\times -d \times\cdots\times(x_i-x_{n-1})\times(x_i-x_n)$
$f_{i+1}(x_{i+1}) = (x_i+d-x_0)\times(x_i-x_0)\times\cdots\times d\times -d \times\cdots\times(x_i-x_{n-2})\times(x_i-x_{n-1})$
比較すると $(x_i+d-x_0)$ が増えて $(x_i-x_n)$ が消えている．したがって $O(1)$ で $f_{i}(x_i)$ から $f_{i+1}(x_{i+1})$ を求められる．

$f_i(T) = (T-x_0)(T-x_1)\cdots(T-x_n)/(T-x_i)$ を計算するには，予め $\prod_i (T-x_i)$ を計算しておいて， $T-x_i$ で割ることで高速に計算できる．

modの割り算が必須なので計算量は全体で $O(n\log \text{mod})$ となる．

// x座標が相異なるn+1点(x_i,y_i)を通るn次以下の多項式f(T)の値を返す
// x_i = a + i*d 0<=i<=n (等差数列)
// O(nlog(MOD))
mint lagrange_interpolation_arithmetic(mint a, mint d, vector<mint> y, mint T) {
    const ll n = y.size() - 1;
    mint ret = 0, ft = 1;
    REP(i, n+1) ft *= T-(a+d*i);
    // f_0(x_0)
    mint f = 1;
    FOR(i, 1, n+1) f *= -1*i*d;
    ret += c[0] * ft / (T-a);
    // f_i(x_i) → f_{i+1}(x_{i+1})
    REP(i, n) {
        f *= d*(i+1) / (d*(i-n));
        ret += y[i+1] / f * ft / (T-a-d*(i+1));
    }
    return ret;
}

ARC033 D - 見たことのない多項式「提出」

例題

ネタバレ注意
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

codeforces Educational Codeforces Round 7 F. The Sum of the k-th Powers

問題ページ
$S(x) = \sum_{i=0}^x i^k \bmod 10^9+7$ とすると答えは $S(n)$ になる． $S(x)$ はk+1次式っぽいので $S(0), S(1), \ldots, S(k+1)$ のk+2点を使ってラグランジュ補間をすれば $S(n)$ が求まる．

答えが多項式の値なことはわかっているが具体的に多項式を構成するのがつらいときに使う

Submission #58554396 - Codeforces

yukicoder No.42 貯金箱の溜息

問題ページ
dp[i番目のコインまで][金額j] = (支払う方法の数) としたdpテーブルでf(m) = dp[5][500m+q] q<500 はmについて5次式になっている（らしい）．f(0)=dp[5][500×0+q], f(1)=dp[5][500×1+q], … , f(5)=dp[5][500×5+q] の6点を用いて多項式fを復元し，f(M/500)を求める．

答えが多項式の値なことはわかっているが具体的に多項式を構成するのがつらいときに使う
(これが多項式だって気づく難易度高すぎない？)

提出 #367653 No.42 貯金箱の溜息 - yukicoder

ライブラリ作ったはいいけど今後使うことはあるのだろうか

2019-07-10

CODE THANKS FESTIVAL 2018 G - Sum of Cards

AtCoder 競技プログラミング

問題ページ

解法

$n$ 頂点のグラフで考える． $i$ 枚目のカードの表に $X$ ，裏に $Y$ が書かれている場合，頂点 $X$ と頂点 $Y$ の間に辺を引く．問題文の条件をこのグラフ上に言い換えると，

表裏を選ぶ操作→各辺を向き付けする．
$k$ 種類以上の整数が見える→出次数が1以上の頂点がk個以上にする．
見えている数の和の最大化→ $\sum_{v} ($ 頂点 $v$ から出ている辺の本数 $)\times v$ の最大化

となる． $a_i, b_i$ は順列になっていることから，このグラフは全頂点の次数が2で，各連結成分は一つのサイクルになっている．各サイクルごとに $j$ 種類使ったときに達成しうる最大値が計算できれば，あとはナップサックDPの要領で $K$ 種類以上の数が見えるときの和の最大値を求められる．したがって，各サイクルごとに $j$ 種類使ったときに達成しうる最大値を計算する方法を考える．

この問題では $k \leq n \leq 5000$ であることから $O(NK)$ 程度の大きさのDPテーブルは持てる．このような問題では $dp \lbrack i \rbrack \lbrack j \rbrack = i$ 番目までで $j$ 種類使ったときの最大値というような状態の持ち方が定石となる．このようにDPテーブルを保持したときに $i, i-1$ 番目の頂点間の辺の向き付けに対応する遷移がどのようになるか考える． $i-1$ 番目の頂点から $i-2$ 番目の頂点に向き付けされていて， $i-1$ 番目から $i$ 番目へ向き付けする場合のみ，種類数 $j$ が増加しない．よって種類数が増加するかどうかの判定のためには，直前の辺の向きをDPテーブルに持っておけば可能となる．サイクルの最後の頂点についての辺の向き付けで種類数が増加するかの判定を行うためには，サイクルの最初の頂点と最後の頂点の間の辺の向きをDPテーブルに持っておけば可能となる．

よって
$dp \lbrack i \rbrack \lbrack j \rbrack \lbrack k \rbrack \lbrack l \rbrack =$ サイクルの $i$ 番目までで $j$ 種類の数を使い直前の辺の向きが $k$ で最初の頂点と最後の頂点の辺の向きが $l$ のときの和の最大値
というDPテーブルを持つことで $i, i-1$ 番目の頂点間の辺の向き付けに対応する遷移を実現できる．具体的な遷移はソースコードを見てください．

まとめると，

グラフを構築してサイクルに分割
サイクルごとにDPして $j$ 種類の数を使ったときの和の最大値を求める
ナップサックDPでサイクルごとの値をまとめて最終的な答えを求める

とすればよい．

これ500点ってマジ？？？

#include <bits/stdc++.h>

using namespace std;
using ll = long long;
// #define int ll
using PII = pair<ll, ll>;

#define FOR(i, a, n) for (ll i = (ll)a; i < (ll)n; ++i)
#define REP(i, n) FOR(i, 0, n)
#define ALL(x) x.begin(), x.end()

template<typename T> T &chmin(T &a, const T &b) { return a = min(a, b); }
template<typename T> T &chmax(T &a, const T &b) { return a = max(a, b); }
template<typename T> bool IN(T a, T b, T x) { return a<=x&&x<b; }
template<typename T> T ceil(T a, T b) { return a/b + !!(a%b); }

template<typename T> vector<T> make_v(size_t a) { return vector<T>(a); }
template<typename T,typename... Ts>
auto make_v(size_t a,Ts... ts) {
    return vector<decltype(make_v<T>(ts...))>(a,make_v<T>(ts...));
}
template<typename T,typename V> typename enable_if<is_class<T>::value==0>::type
fill_v(T &t, const V &v) { t=v; }
template<typename T,typename V> typename enable_if<is_class<T>::value!=0>::type
fill_v(T &t, const V &v ) { for(auto &e:t) fill_v(e,v); }

template<class S,class T>
ostream &operator <<(ostream& out,const pair<S,T>& a) {
    out<<'('<<a.first<<','<<a.second<<')'; return out;
}
template<class T>
ostream &operator <<(ostream& out,const vector<T>& a){
    out<<'[';
    for(const T &i: a) out<<i<<',';
    out<<']';
    return out;
}
template<class T>
ostream &operator <<(ostream& out, const set<T>& a) {
    out<<'{';
    for(const T &i: a) out<<i<<',';
    out<<'}';
    return out;
}
template<class T, class S>
ostream &operator <<(ostream& out, const map<T,S>& a) {
    out<<'{';
    for(auto &i: a) out<<i<<',';
    out<<'}';
    return out;
}

int dx[] = {0, 1, 0, -1}, dy[] = {1, 0, -1, 0}; // DRUL
const int INF = 1<<30;
const ll LLINF = 1LL<<60;
const ll MOD = 1000000007;

ll dp[5010][5010][2][2], x[5010][5010];
signed main(void)
{
    cin.tie(0);
    ios::sync_with_stdio(false);

    ll n, K;
    cin >> n >> K;
    vector<ll> a(n), b(n);
    REP(i, n) cin >> a[i], a[i]--;
    REP(i, n) cin >> b[i], b[i]--;

    vector<vector<ll>> g(n);
    REP(i, n) {
        g[a[i]].push_back(b[i]);
        g[b[i]].push_back(a[i]);
    }

    ll idx = 0;
    vector<vector<ll>> vs;
    vector<bool> used(n);
    function<void(ll)> dfs = [&](ll v) {
        used[v] = true;
        vs[idx].push_back(v+1);
        for(auto to: g[v]) {
            if(!used[to]) dfs(to);
        }
    };
    REP(i, n) {
        if(!used[i]) {
            vs.push_back(vector<ll>());
            dfs(i);
            idx++;
        }
    }

    memset(dp, -1, sizeof(dp));
    idx = 0;
    vector<vector<ll>> dp2(vs.size());
    for(auto v: vs) {
        // サイクルvについてDP
        const ll m = v.size();
        dp[0][1][1][1] = v[m-1];
        dp[0][1][0][0] = v[0];
        FOR(i, 1, m) FOR(j, 1, m+1) REP(k, 2) {
            if(dp[i-1][j][0][k] != -1) {
                chmax(dp[i][j][1][k], dp[i-1][j][0][k] + v[i-1]);
                if(i==m-1 && k==1) {
                    chmax(dp[i][j][0][k], dp[i-1][j][0][k] + v[i]);
                } else {
                    chmax(dp[i][j+1][0][k], dp[i-1][j][0][k] + v[i]);
                }
            }
            if(dp[i-1][j][1][k] != -1) {
                chmax(dp[i][j+1][1][k], dp[i-1][j][1][k] + v[i-1]);
                if(i == m-1 && k==1) {
                    chmax(dp[i][j][0][k], dp[i-1][j][1][k] + v[i]);
                } else {
                    chmax(dp[i][j+1][0][k], dp[i-1][j][1][k] + v[i]);
                }
            }
        }
        // dp2[i番目のサイクル][j種類使った] = 和の最大値
        dp2[idx].resize(v.size()+1);
        REP(i, m) REP(j, 2) REP(k, 2) {
            chmax(dp2[idx][i+1], dp[m-1][i+1][j][k]);
        }
        idx++;
        // dpの初期化
        REP(i, m) FOR(j, 1, m+1) REP(k, 2) REP(l, 2) {
            dp[i][j][k][l] = -1;
        }
    }

    // ナップサックDPの要領で連結成分ごとの値をまとめる
    memset(x, -1, sizeof(x));
    x[0][0] = 0;
    REP(i, dp2.size()) REP(j, K+1) REP(k, dp2[i].size()) {
        if(x[i][j] == -1) continue;
        chmax(x[i+1][min(j+k, K)], x[i][j] + dp2[i][k]);
    }
    cout << x[vs.size()][K] << endl;

    return 0;
}

2019-06-02

M-SOLUTIONS プロコンオープン C - Best-of-(2n-1)

競技プログラミング AtCoder

問題ページ

解法

$a = \frac{A}{100}, b = \frac{B}{100}, c = \frac{C}{100} = 1-a-b$ とする．

高橋くんが勝つのが $n$ 回，青木くんが勝つのが $i$ 回，引き分けが $j$ 回起きるとする．

期待値の前にまず確率がどのようになるか考える．高橋くんが最後に勝つのは確定で，それ以外の部分は確率 $a$ の操作が $n-1$ 回，確率 $b$ の操作が $i$ 回，確率 $c$ の操作が $j$ 回起きるような事象の確率である．高橋くんが勝つ確率は $a$ で，後半の事象の確率は独立試行であることを用いて $\frac{(n-1+a+b)!}{a!b!(n-1)!} a^{n-1} b^{i} c^{j}$ となる．よって確率は $\frac{(n-1+a+b)!}{a!b!(n-1)!} a^{n} b^{i} c^{j}$ となる．

期待値の定義から確率とゲームの回数の積を足し合わせることで期待値を計算すると $\sum_{i=0}^{n-1} \sum_{j=0}^{\infty} \frac{(n-1+i+j)!}{i!j!(n-1)!} a^{n} b^{i} c^{j} \times (n+i+j) = \sum_{i=0}^{n-1} \sum_{j=0}^{\infty} \frac{(n+i+j)!}{i!j!(n-1)!} a^{n} b^{i} (1-a-b)^{j}$ となる．無限級数の部分をWolframAlpha先生に計算してもらうと $\sum_{j=0}^{\infty} \frac{(i+j+n)!}{i! j! (n-1)!)} a^{n} b^{i} (1-a-b)^{j} = \frac{a^{n} b^{i} (i+n)! }{ i! (n-1)! (a+b)^{n+1+i} }$ と閉じた形になる．あとは $O(n)$ で和を計算すれば期待値が求まる．
https://ja.wolframalpha.com/input/?i=sum[(i%2Bj%2Bn)!%2F(i!j!(n-1)!)+aⁿ+bⁱ+(1-a-b)^j,+{j,+0,+inf}]&assumption="i"+->+"Variable"

青木くんが勝つ場合についても同様に計算でき，足し合わせることで答えが求まる．

#include <bits/stdc++.h>

using namespace std;
using ll = long long;
// #define int ll
using PII = pair<ll, ll>;

#define FOR(i, a, n) for (ll i = (ll)a; i < (ll)n; ++i)
#define REP(i, n) FOR(i, 0, n)
#define ALL(x) x.begin(), x.end()

template<typename T> T &chmin(T &a, const T &b) { return a = min(a, b); }
template<typename T> T &chmax(T &a, const T &b) { return a = max(a, b); }
template<typename T> bool IN(T a, T b, T x) { return a<=x&&x<b; }
template<typename T> T ceil(T a, T b) { return a/b + !!(a%b); }

template<typename T> vector<T> make_v(size_t a) { return vector<T>(a); }
template<typename T,typename... Ts>
auto make_v(size_t a,Ts... ts) {
    return vector<decltype(make_v<T>(ts...))>(a,make_v<T>(ts...));
}
template<typename T,typename V> typename enable_if<is_class<T>::value==0>::type
fill_v(T &t, const V &v) { t=v; }
template<typename T,typename V> typename enable_if<is_class<T>::value!=0>::type
fill_v(T &t, const V &v ) { for(auto &e:t) fill_v(e,v); }

template<class S,class T>
ostream &operator <<(ostream& out,const pair<S,T>& a) {
    out<<'('<<a.first<<','<<a.second<<')'; return out;
}
template<class T>
ostream &operator <<(ostream& out,const vector<T>& a){
    out<<'[';
    for(const T &i: a) out<<i<<',';
    out<<']';
    return out;
}
template<class T>
ostream &operator <<(ostream& out, const set<T>& a) {
    out<<'{';
    for(const T &i: a) out<<i<<',';
    out<<'}';
    return out;
}
template<class T, class S>
ostream &operator <<(ostream& out, const map<T,S>& a) {
    out<<'{';
    for(auto &i: a) out<<i<<',';
    out<<'}';
    return out;
}

int dx[] = {0, 1, 0, -1}, dy[] = {1, 0, -1, 0}; // DRUL
const int INF = 1<<30;
const ll LLINF = 1LL<<60;
const ll MOD = 1000000007;

template<ll MOD>
struct modint {
    ll x;
    modint(): x(0) {}
    modint(ll y) : x(y>=0 ? y%MOD : y%MOD+MOD) {}
    static constexpr ll mod() { return MOD; }
    friend modint pow(modint x, ll e) {
        modint a = 1;
        while(e > 0) {
            if(e%2 == 0) {x *= x; e /= 2;}
            else {a *= x; e--;}
        }
        return a;
    }
    modint inv() const {
        ll a=x, b=MOD, u=1, y=1, v=0, z=0;
        while(a) {
            ll q = b/a;
            swap(z -= q*u, u);
            swap(y -= q*v, v);
            swap(b -= q*a, a);
        }
        return z;
    }
    // Comparators
    bool operator <(modint b) { return x < b.x; }
    bool operator >(modint b) { return x > b.x; }
    bool operator<=(modint b) { return x <= b.x; }
    bool operator>=(modint b) { return x >= b.x; }
    bool operator!=(modint b) { return x != b.x; }
    bool operator==(modint b) { return x == b.x; }
    // Basic Operations
    modint operator+(modint r) const { return modint(*this) += r; }
    modint operator-(modint r) const { return modint(*this) -= r; }
    modint operator*(modint r) const { return modint(*this) *= r; }
    modint operator/(modint r) const { return modint(*this) /= r; }
    modint &operator+=(modint r) {
        if((x += r.x) >= MOD) x -= MOD;
        return *this;
    }
    modint &operator-=(modint r) {
        if((x -= r.x) < 0) x += MOD;
        return *this;
    }
    modint &operator*=(modint r) {
    #if !defined(_WIN32) || defined(_WIN64)
        x = x * r.x % MOD; return *this;
    #endif
        unsigned long long y = x * r.x;
        unsigned xh = (unsigned) (y >> 32), xl = (unsigned) y, d, m;
        asm(
            "divl %4; \n\t"
            : "=a" (d), "=d" (m)
            : "d" (xh), "a" (xl), "r" (MOD)
        );
        x = m;
        return *this;
    }
    modint &operator/=(modint r) { return *this *= r.inv(); }
    // increment, decrement
    modint operator++() { x++; return *this; }
    modint operator++(signed) { modint t = *this; x++; return t; }
    modint operator--() { x--; return *this; }
    modint operator--(signed) { modint t = *this; x--; return t; }
};
using mint = modint<1000000007>;
template<class T> mint operator*(T l, mint r) { return mint(l) *= r; }
template<class T> mint operator+(T l, mint r) { return mint(l) += r; }
template<class T> mint operator-(T l, mint r) { return mint(l) -= r; }
template<class T> mint operator/(T l, mint r) { return mint(l) /= r; }
template<class T> bool operator==(T l, mint r) { return mint(l) == r; }
template<class T> bool operator!=(T l, mint r) { return mint(l) != r; }
// Input/Output
ostream &operator<<(ostream& os, mint a) { return os << a.x; }
istream &operator>>(istream& is, mint &a) { return is >> a.x; }
string to_frac(mint v) {
    static map<ll, PII> mp;
    if(mp.empty()) {
        mp[0] = mp[mint::mod()] = {0, 1};
        FOR(i, 2, 1001) FOR(j, 1, i) if(__gcd(i, j) == 1) {
            mp[(mint(i) / j).x] = {i, j};
        }
    }
    auto itr = mp.lower_bound(v.x);
    if(itr != mp.begin() && v.x - prev(itr)->first < itr->first - v.x) --itr;
    string ret = to_string(itr->second.first + itr->second.second * ((int)v.x - itr->first));
    if(itr->second.second > 1) {
        ret += '/';
        ret += to_string(itr->second.second);
    }
    return ret;
}

signed main(void)
{
    cin.tie(0);
    ios::sync_with_stdio(false);

    ll n, aa, bb, cc;
    cin >> n >> aa >> bb >> cc;

    mint fact = 1;
    FOR(i, 1, n) fact *= i;
    mint a(aa), b(bb), c(cc);
    a /= 100, b /= 100, c /= 100;

    mint ret = 0;
    mint x = 1, y = 1;
    FOR(i, 1, n+1) x *= i;
    REP(i, n) {
        if(i) x *= n+i, y *= i;
        ret += pow(a, n) * pow(b, i) * x / pow(a+b, i+n+1) / y / fact;
    }
    x = 1, y = 1;
    FOR(i, 1, n+1) x *= i;
    REP(i, n) {
        if(i) x *= n+i, y *= i;
        ret += pow(b, n) * pow(a, i) * x / pow(a+b, i+n+1) / y / fact;
    }

    cout << ret << endl;

    return 0;
}

ferinの競プロ帳

競プロについてのメモ

yukicoder No.878 Range High-Element Query

解法

yukicoder No.877 Range ReLU Query

解法

CODE FESTIVAL 2016 Grand Final J - 123 Pairs

解法

TTPC2019参加記

コンテスト

B問題

A問題

D問題

C問題

E問題

F問題

G問題

H問題

O問題

H問題

G問題

M問題

G問題

ラグランジュ補間

$f(T)$ を一つ求める ( $T$ はgiven)

$f(x)$ の係数を求める

与えられる点の座標が等差数列

$f(T)$ を一つ求める (Tはgiven)

例題

codeforces Educational Codeforces Round 7 F. The Sum of the k-th Powers

yukicoder No.42 貯金箱の溜息

CODE THANKS FESTIVAL 2018 G - Sum of Cards

解法

M-SOLUTIONS プロコンオープン C - Best-of-(2n-1)

解法

解法

解法

解法

コンテスト

B問題

A問題

D問題

C問題

E問題

F問題

G問題

H問題

O問題

H問題

G問題

M問題

G問題

を一つ求める (はgiven)

の係数を求める

与えられる点の座標が等差数列

を一つ求める (Tはgiven)

例題

codeforces Educational Codeforces Round 7 F. The Sum of the k-th Powers

yukicoder No.42 貯金箱の溜息

解法

解法

$f(T)$ を一つ求める ( $T$ はgiven)

$f(x)$ の係数を求める

$f(T)$ を一つ求める (Tはgiven)