ferinの競プロ帳

競プロについてのメモ

AGC029 D - Grid game

競技プログラミング AtCoder

問題ページ

解法

高橋くんが動かなかった場合、青木くんも動かなければゲームが終了するので高橋くんは動けるならば動くべきである。各行について駒がたどりつける最大の列txが求まっていたとする。このときtx以下の地点に障害物が存在していればその障害物の上に駒を誘導することでゲームを終了できる。各行について障害物の存在する列を要素としたsetを保持しておけばupper_boundでset中にtx以下の要素が含まれているかの判定は可能である。txの更新はその行のtx+1に障害物がなければ+1、あれば移動できないので-1とすればよい。上の行から順番に見ていき障害物に当たれる場所が存在した時点でその行を答えとして出力すればよい。

#include <bits/stdc++.h>

using namespace std;
using ll = long long;
// #define int ll
using PII = pair<int, int>;

#define FOR(i, a, n) for (ll i = (ll)a; i < (ll)n; ++i)
#define REP(i, n) FOR(i, 0, n)
#define ALL(x) x.begin(), x.end()

template<typename T> T &chmin(T &a, const T &b) { return a = min(a, b); }
template<typename T> T &chmax(T &a, const T &b) { return a = max(a, b); }
template<typename T> bool IN(T a, T b, T x) { return a<=x&&x<b; }
template<typename T> T ceil(T a, T b) { return a/b + !!(a%b); }

template<typename T> vector<T> make_v(size_t a) { return vector<T>(a); }
template<typename T,typename... Ts>
auto make_v(size_t a,Ts... ts) {
  return vector<decltype(make_v<T>(ts...))>(a,make_v<T>(ts...));
}
template<typename T,typename V> typename enable_if<is_class<T>::value==0>::type
fill_v(T &t, const V &v) { t=v; }
template<typename T,typename V> typename enable_if<is_class<T>::value!=0>::type
fill_v(T &t, const V &v ) { for(auto &e:t) fill_v(e,v); }

template<class S,class T>
ostream &operator <<(ostream& out,const pair<S,T>& a){
  out<<'('<<a.first<<','<<a.second<<')'; return out;
}
template<typename T>
istream& operator >> (istream& is, vector<T>& vec){
  for(T& x: vec) {is >> x;} return is;
}
template<class T>
ostream &operator <<(ostream& out,const vector<T>& a){
  out<<'['; for(T i: a) {out<<i<<',';} out<<']'; return out;
}

int dx[] = {0, 1, 0, -1}, dy[] = {1, 0, -1, 0}; // DRUL
const int INF = 1<<30;
const ll LLINF = 1LL<<60;
const int MOD = 1000000007;

signed main(void)
{
  cin.tie(0);
  ios::sync_with_stdio(false);

  ll h, w, n;
  cin >> h >> w >> n;
  vector<ll> x(n), y(n);
  REP(i, n) cin >> y[i] >> x[i], y[i]--, x[i]--;

  vector<set<ll>> v(h);
  REP(i, n) {
    v[y[i]].insert(x[i]);
  }

  ll tx = 0;
  FOR(i, 1, h) {
    // v[i]にtx以下の要素が含まれているか
    if(v[i].upper_bound(tx) != v[i].begin()) {
      cout << i << endl;
      return 0;
    }

    if(v[i].find(tx+1) != v[i].end()) {

    } else {
      tx++;
    }
  }

  cout << h << endl;

  return 0;
}

AGC029 B - Powers of two

AtCoder 競技プログラミング

問題ページ

解法

各値を頂点に持ち、値を足すと2べきになる頂点間に辺を張るとする。このグラフで最大マッチングが求められればいいが、N<=10^5だと二部マッチングでもTLEしそうなので貪欲なりDPなりでマッチングを高速に求められる構造がなければできなさそう。グラフを色々書いて実験しているとグラフが森にしかならない。2数x,yに対してx+zもy+zも2べきになるような数zは高々一つしか存在しないことが言えるので全てのグラフについて森になることが言えた。マッチングする対象が1つだけ存在する頂点(=葉)が存在したときにその頂点をマッチングに含めないことで解が改善されることは存在しない。したがって葉から貪欲に取っていくことで最大マッチングが求まる。

2t - a[i]の値で分類するとか色々迷走して時間を溶かした…もうちょっと早く解きたい

#include <bits/stdc++.h>

using namespace std;
using ll = long long;
// #define int ll
using PII = pair<ll, ll>;

#define FOR(i, a, n) for (ll i = (ll)a; i < (ll)n; ++i)
#define REP(i, n) FOR(i, 0, n)
#define ALL(x) x.begin(), x.end()

template<typename T> T &chmin(T &a, const T &b) { return a = min(a, b); }
template<typename T> T &chmax(T &a, const T &b) { return a = max(a, b); }
template<typename T> bool IN(T a, T b, T x) { return a<=x&&x<b; }
template<typename T> T ceil(T a, T b) { return a/b + !!(a%b); }

template<typename T> vector<T> make_v(size_t a) { return vector<T>(a); }
template<typename T,typename... Ts>
auto make_v(size_t a,Ts... ts) {
  return vector<decltype(make_v<T>(ts...))>(a,make_v<T>(ts...));
}
template<typename T,typename V> typename enable_if<is_class<T>::value==0>::type
fill_v(T &t, const V &v) { t=v; }
template<typename T,typename V> typename enable_if<is_class<T>::value!=0>::type
fill_v(T &t, const V &v ) { for(auto &e:t) fill_v(e,v); }

template<class S,class T>
ostream &operator <<(ostream& out,const pair<S,T>& a){
  out<<'('<<a.first<<','<<a.second<<')'; return out;
}
template<typename T>
istream& operator >> (istream& is, vector<T>& vec){
  for(T& x: vec) {is >> x;} return is;
}
template<class T>
ostream &operator <<(ostream& out,const vector<T>& a){
  out<<'['; for(T i: a) {out<<i<<',';} out<<']'; return out;
}

int dx[] = {0, 1, 0, -1}, dy[] = {1, 0, -1, 0}; // DRUL
const int INF = 1<<30;
const ll LLINF = 1LL<<60;
const ll MOD = 1000000007;

signed main(void)
{
  cin.tie(0);
  ios::sync_with_stdio(false);

  ll n;
  cin >> n;
  vector<ll> a(n);
  map<ll,ll> mp, cnt;
  REP(i, n) {
    cin >> a[i];
    mp[a[i]]++;
    cnt[a[i]]++;
  }

  vector<ll> pow2(31);
  pow2[0] = 1;
  FOR(i, 1, 31) pow2[i] = pow2[i-1] * 2;

  sort(ALL(a));
  a.erase(unique(ALL(a)), a.end());
  reverse(ALL(a));

  ll ret = 0;
  REP(i, n) {
    REP(j, 31) {
      if(pow2[j] < a[i]) continue;
      if(a[i]*2 == pow2[j]) {
        ll tmp = mp[a[i]] / 2;
        mp[a[i]] -= tmp * 2;
        ret += tmp;
        continue;
      }
      if(mp.find(pow2[j] - a[i]) != mp.end()) {
        ll tmp = min(mp[pow2[j] - a[i]], mp[a[i]]);
        mp[pow2[j] - a[i]] -= tmp;
        mp[a[i]] -= tmp;
        ret += tmp;
      }
    }
  }

  cout << ret << endl;

  return 0;
}

AGC029 A - Irreversible operation

AtCoder 競技プログラミング

問題ページ

解法

操作を終えたあとの最終的な文字列がどうなっているか考えます。BWと並んでいるところがあればまだ操作が続くはずなので一度Bが出てきた後にWがでてくることはありません。したがって最終的な文字列はWW…WWBB…BBとなるはずです。Wの前にBが存在していればそのBとswapするはずなので、各WについてそのWより前にあるBの数を数えることで答えが求まります。

#include <bits/stdc++.h>

using namespace std;
using ll = long long;
// #define int ll
using PII = pair<ll, ll>;

#define FOR(i, a, n) for (ll i = (ll)a; i < (ll)n; ++i)
#define REP(i, n) FOR(i, 0, n)
#define ALL(x) x.begin(), x.end()

template<typename T> T &chmin(T &a, const T &b) { return a = min(a, b); }
template<typename T> T &chmax(T &a, const T &b) { return a = max(a, b); }
template<typename T> bool IN(T a, T b, T x) { return a<=x&&x<b; }
template<typename T> T ceil(T a, T b) { return a/b + !!(a%b); }

template<typename T> vector<T> make_v(size_t a) { return vector<T>(a); }
template<typename T,typename... Ts>
auto make_v(size_t a,Ts... ts) {
  return vector<decltype(make_v<T>(ts...))>(a,make_v<T>(ts...));
}
template<typename T,typename V> typename enable_if<is_class<T>::value==0>::type
fill_v(T &t, const V &v) { t=v; }
template<typename T,typename V> typename enable_if<is_class<T>::value!=0>::type
fill_v(T &t, const V &v ) { for(auto &e:t) fill_v(e,v); }

template<class S,class T>
ostream &operator <<(ostream& out,const pair<S,T>& a){
  out<<'('<<a.first<<','<<a.second<<')'; return out;
}
template<typename T>
istream& operator >> (istream& is, vector<T>& vec){
  for(T& x: vec) {is >> x;} return is;
}
template<class T>
ostream &operator <<(ostream& out,const vector<T>& a){
  out<<'['; for(T i: a) {out<<i<<',';} out<<']'; return out;
}

int dx[] = {0, 1, 0, -1}, dy[] = {1, 0, -1, 0}; // DRUL
const int INF = 1<<30;
const ll LLINF = 1LL<<60;
const ll MOD = 1000000007;

signed main(void)
{
  cin.tie(0);
  ios::sync_with_stdio(false);

  string s;
  cin >> s;
  int n = s.size();

  ll ret = 0, tmp = 0;
  REP(i, n) {
    if(s[i] == 'B') {
      tmp++;
    } else {
      ret += tmp;
    }
  }
  cout << ret << endl;

  return 0;
}

天下一プログラマーコンテスト2015本戦　E - 天下一コップ

競技プログラミング AtCoder

問題ページ

解法

順列全てや部分列それぞれについて計算しろといった問題で与えられた通りに数えるのはTLEしてしまうので別の視点から数え上げるのが有効な場合が多い。今回の問題ではi番目の長方形が底でj番目の長方形の高さまで水が入っているような並び方が何通りあるか？という視点で考えてみる。f(i,j) = (i番目の長方形が底でj番目の長方形の高さまで水が入っているような並び方の数) とすると答えは \displaystyle{\sum_{i,j} W_i (H_j - H_i) f(i,j)} となる。ここで {H_j} < {H_i}であるような場合について場合分けするのは大変なのであらかじめ高さで降順にソートしておきj<iとなるようなi,jの組についてしか計算しないとする。
条件を満たすような並び方がどのような並び方かについて考える。i番目の長方形を中間においたときにj番目がある側と反対側にj番目より高い長方形が集まっていれば条件を満たす。j番目より高い長方形がj番目と同じ側に存在しているとi番目の長方形にj番目の長方形の高さより高い位置まで水が貯まるのでこれを数えてはいけない。
f:id:ferin_tech:20181215180609p:plain
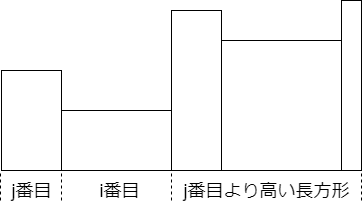
f(i,j)を高速に求める方法として確率の考え方を用いる。全通りについて計算しているので確率 * N!を計算すれば並び方の数を計算できる。高い長方形から順番に挿入していくと考える。j番目より高い長方形がすでに存在しているところにj番目の長方形を追加できる場所はj+1通りある。このうち両端の2箇所に挿入した場合のみ条件を満たす。i番目の長方形を挿入する位置はi+2箇所あり、そのうちj番目の長方形に挟まれる1箇所のみが条件を満たす。まとめると条件を満たす確率は2/(j+1)(j+2)となる。 f:id:ferin_tech:20181215180626p:plain
よって答えは sum(Wi/(j+1)(j+2)) * 2N! (0 <= j < i < n) となる。この式を愚直に計算するとO(N^2)となるのでこの計算を高速化する。iとjについて混ざった式になっているのでiとjについて独立な式にすることを考える。sum(W[i] * (sum(H[j]/(j+1)(j+2)) + H[i] * sum(1/(j+1)(j+2)))) 2N!となる。この式のうちsum(H[j]/(j+1)(j+2))とsum(1/(j+1)(j+2))は事前に計算しておくことでO(1)で計算できる。したがって全体でO(N)でこの式を計算することができ問題を解くことができた。

#include <bits/stdc++.h>

using namespace std;
using ll = long long;
// #define int ll
using PII = pair<ll, ll>;

#define FOR(i, a, n) for (ll i = (ll)a; i < (ll)n; ++i)
#define REP(i, n) FOR(i, 0, n)
#define ALL(x) x.begin(), x.end()

template<typename T> T &chmin(T &a, const T &b) { return a = min(a, b); }
template<typename T> T &chmax(T &a, const T &b) { return a = max(a, b); }
template<typename T> bool IN(T a, T b, T x) { return a<=x&&x<b; }
template<typename T> T ceil(T a, T b) { return a/b + !!(a%b); }

template<typename T> vector<T> make_v(size_t a) { return vector<T>(a); }
template<typename T,typename... Ts>
auto make_v(size_t a,Ts... ts) {
  return vector<decltype(make_v<T>(ts...))>(a,make_v<T>(ts...));
}
template<typename T,typename V> typename enable_if<is_class<T>::value==0>::type
fill_v(T &t, const V &v) { t=v; }
template<typename T,typename V> typename enable_if<is_class<T>::value!=0>::type
fill_v(T &t, const V &v ) { for(auto &e:t) fill_v(e,v); }

template<class S,class T>
ostream &operator <<(ostream& out,const pair<S,T>& a){
  out<<'('<<a.first<<','<<a.second<<')'; return out;
}
template<typename T>
istream& operator >> (istream& is, vector<T>& vec){
  for(T& x: vec) {is >> x;} return is;
}
template<class T>
ostream &operator <<(ostream& out,const vector<T>& a){
  out<<'['; for(T i: a) {out<<i<<',';} out<<']'; return out;
}

int dx[] = {0, 1, 0, -1}, dy[] = {1, 0, -1, 0}; // DRUL
const int INF = 1<<30;
const ll LLINF = 1LL<<60;
const ll MOD = 1000000007;

// 二分累乗 O(funcの計算量*logE)
template<typename T=ll>
T binpow(T x, ll e, function<T(T,T)> func=[](T a, T b){return a*b%MOD;}, T d=1) {
  T ret = d, p = x;
  while(e > 0) {
    if(e%2 == 0) {p = func(p, p); e /= 2;}
    else {ret = func(ret, p); e--;}
  }
  return ret;
};

struct mint {
  ll x;
  mint(): x(0) { }
  mint(ll y) : x(y>=0 ? y%MOD : y%MOD+MOD) {}
  ll get() const { return x; }
  // e乗
  mint pow(ll e) {
    ll a = 1, p = x;
    while(e > 0) {
      if(e%2 == 0) {p = (p*p) % MOD; e /= 2;}
      else {a = (a*p) % MOD; e--;}
    }
    return mint(a);
  }
  // Comparators
  bool operator <(mint b) { return x < b.x; }
  bool operator >(mint b) { return x > b.x; }
  bool operator<=(mint b) { return x <= b.x; }
  bool operator>=(mint b) { return x >= b.x; }
  bool operator!=(mint b) { return x != b.x; }
  bool operator==(mint b) { return x == b.x; }
  // increment, decrement
  mint operator++() { x++; return *this; }
  mint operator++(signed) { mint t = *this; x++; return t; }
  mint operator--() { x--; return *this; }
  mint operator--(signed) { mint t = *this; x--; return t; }
  // Basic Operations
  mint &operator+=(mint that) {
    x += that.x;
    if(x >= MOD) x -= MOD;
    return *this;
  }
  mint &operator-=(mint that) {
    x -= that.x;
    if(x < 0) x += MOD;
    return *this;
  }
  mint &operator*=(mint that) {
    x = (ll)x * that.x % MOD;
    return *this;
  }
  mint &operator/=(mint that) {
    x = (ll)x * that.pow(MOD-2).x % MOD;
    return *this;
  }
  mint &operator%=(mint that) {
    x = (ll)x % that.x;
    return *this;
  }
  mint operator+(mint that) const { return mint(*this) += that; }
  mint operator-(mint that) const { return mint(*this) -= that; }
  mint operator*(mint that) const { return mint(*this) *= that; }
  mint operator/(mint that) const { return mint(*this) /= that; }
  mint operator%(mint that) const { return mint(*this) %= that; }
};
// Input/Output
ostream &operator<<(ostream& os, mint a) { return os << a.x; }
istream &operator>>(istream& is, mint &a) { return is >> a.x; }

signed main(void)
{
  cin.tie(0);
  ios::sync_with_stdio(false);

  ll n;
  cin >> n;
  vector<PII> a(n);
  REP(i, n) cin >> a[i].second >> a[i].first;

  sort(ALL(a), greater<>());
  vector<mint> w(n), h(n);
  REP(i, n) w[i] = a[i].second, h[i] = a[i].first;

  vector<mint> p(n), q(n);
  p[0] = mint(h[0] * binpow(2, MOD-2));
  FOR(i, 1, n) p[i] = p[i-1] + h[i] * binpow((i+1)*(i+2)%MOD, MOD-2);
  q[0] = mint(binpow(2, MOD-2));
  FOR(i, 1, n) q[i] = q[i-1] + binpow((i+1)*(i+2)%MOD, MOD-2);

  mint ans = 0;
  REP(i, n) ans += (p[i] - q[i] * h[i]) * w[i];
  ans *= 2;
  REP(i, n) ans *= i+1;

  cout << ans << endl;

  return 0;
}

Educational Codeforces Round 55 (Rated for Div. 2) E. Increasing Frequency

競技プログラミング Codeforces

問題ページ

解法

ある区間[l,r]を選択したときに最適なkの値について考える。[l,r]の中で最も出現頻度が多い値がcになるようにkを設定すればよい。したがって区間[l,r]に操作をしたときの答えは([l,r]以外のcの数) + ([l,r]で出現頻度が最も多い回数) - ([l,r]のcの数)となる。区間の左端をlとしたときにrを増やして出現頻度を増やせると答えが+1され、rを増やしたときにcが区間中に入ってしまうと答えが-1される。
数列中にcとa(a!=c)しか存在しないとして考える。aを+1、cを-1とした数列に置き換えると(答え)=(cの数)-(区間和の最大)となる。実際には値の種類が5*10^5種類あるが値aとcだけについての数列を各aに対して作成し、各数列に対して最適解を求めmaxを取ればよい。
値aと値cに対しての数列をつくる方法について考える。値aと値cが存在する位置を覚える変数g[a]とg[c]を用意しておく。idx_aとidx_cを保持しておきこれを更新していく。この更新はidx_a = g[c][idx_c]より大きい最小のindexとして更新できる。詳しくはソースコードを見てください。最初に現れるのがaかcかで場合分けするのが面倒だったので数列の最初にcを追加しておいて最後に答えから1を引くとして実装した。区間和の最大を取得するには累積和を取った配列xと後ろから累積maxを取った配列yを用意しておきmax(y[i] - x[i-1])を見ればよい。
数列の要素数の合計はO(N)程度で収まるのでこれで解ける。

#include <bits/stdc++.h>

using namespace std;
using ll = long long;
// #define int ll
using PII = pair<ll, ll>;

#define FOR(i, a, n) for (ll i = (ll)a; i < (ll)n; ++i)
#define REP(i, n) FOR(i, 0, n)
#define ALL(x) x.begin(), x.end()

template<typename T> T &chmin(T &a, const T &b) { return a = min(a, b); }
template<typename T> T &chmax(T &a, const T &b) { return a = max(a, b); }
template<typename T> bool IN(T a, T b, T x) { return a<=x&&x<b; }
template<typename T> T ceil(T a, T b) { return a/b + !!(a%b); }

template<typename T> vector<T> make_v(size_t a) { return vector<T>(a); }
template<typename T,typename... Ts>
auto make_v(size_t a,Ts... ts) {
  return vector<decltype(make_v<T>(ts...))>(a,make_v<T>(ts...));
}
template<typename T,typename V> typename enable_if<is_class<T>::value==0>::type
fill_v(T &t, const V &v) { t=v; }
template<typename T,typename V> typename enable_if<is_class<T>::value!=0>::type
fill_v(T &t, const V &v ) { for(auto &e:t) fill_v(e,v); }

template<class S,class T>
ostream &operator <<(ostream& out,const pair<S,T>& a){
  out<<'('<<a.first<<','<<a.second<<')'; return out;
}
template<typename T>
istream& operator >> (istream& is, vector<T>& vec){
  for(T& x: vec) {is >> x;} return is;
}
template<class T>
ostream &operator <<(ostream& out,const vector<T>& a){
  out<<'['; for(T i: a) {out<<i<<',';} out<<']'; return out;
}

int dx[] = {0, 1, 0, -1}, dy[] = {1, 0, -1, 0}; // DRUL
const int INF = 1<<30;
const ll LLINF = 1LL<<60;
const ll MOD = 1000000007;

signed main(void)
{
  cin.tie(0);
  ios::sync_with_stdio(false);

  ll n, c;
  cin >> n >> c;
  vector<ll> v(n+1);
  v[0] = c;
  REP(i, n) cin >> v[i+1];

  ll cnum = 0;
  vector<ll> vv(v);
  sort(ALL(vv));
  vv.erase(unique(ALL(vv)), vv.end());
  ll m = 0;
  REP(i, n+1) {
    v[i] = lower_bound(ALL(vv), v[i]) - vv.begin();
    chmax(m, v[i]);
    if(v[i] == v[0]) cnum++;
  }
  c = v[0];

  ll ret = cnum;
  vector<vector<ll>> g(m+1);
  REP(i, n+1) g[v[i]].push_back(i);
  REP(i, m+1) {
    if(i == c) continue;

    vector<ll> x;
    ll idxc = 0, idx;
    ll prevc = 0, prev = -1;
    while(true) {
      idx = upper_bound(ALL(g[i]), g[c][idxc]) - g[i].begin();
      if(idx == g[i].size()) {
        x.push_back(g[i].size() - prev);
        x.push_back(-(ll)g[c].size() + prevc);
        break;
      }
      if(idxc != 0) x.push_back(idx - prev);
      prev = idx;

      idxc = upper_bound(ALL(g[c]), g[i][idx]) - g[c].begin();
      if(idxc == g[c].size()) {
        x.push_back(-(ll)g[c].size() + prevc);
        x.push_back(g[i].size() - prev);
        break;
      }
      x.push_back(-idxc + prevc);
      prevc = idxc;
    }

    FOR(j, 1, x.size()) x[j] += x[j-1];
    vector<ll> y(x);
    for(ll j=(ll)y.size()-2; j>=0; --j) {
      chmax(y[j], y[j+1]);
    }
    ll ma = 0;
    REP(j, x.size()) {
      chmax(ma, cnum + y[j] - (j==0?0:x[j-1]));
    }
    chmax(ret, ma);
  }

  cout << ret-1 << endl;

  return 0;
}

Technocup 2019 - Elimination Round 3 D. Barcelonian Distance

Codeforces 競技プログラミング

問題ページ

解法

最短経路としてあり得るのは直線ax+by+c=0に高々1回乗るような経路しかありえない。x=sxかy=sy上を移動したあと直線上を移動しx=gxかy=gy上を移動するパターンか直線上を移動せずに距離abs(sx-gx)+abs(sy-gy)を移動するようなパターンをすべて試せばよい。直線を移動するパターンでも4通りしか移動方法はありえないので問題なく試せる。

実装を単純化できますか？みたいな問題
直線の傾きとかsx<syとかで場合分けをはじめて地獄を見た

#include <bits/stdc++.h>
 
using namespace std;
using ll = long long;
// #define int ll
using PII = pair<ll, ll>;
 
#define FOR(i, a, n) for (ll i = (ll)a; i < (ll)n; ++i)
#define REP(i, n) FOR(i, 0, n)
#define ALL(x) x.begin(), x.end()
 
template<typename T> T &chmin(T &a, const T &b) { return a = min(a, b); }
template<typename T> T &chmax(T &a, const T &b) { return a = max(a, b); }
template<typename T> bool IN(T a, T b, T x) { return a<=x&&x<b; }
template<typename T> T ceil(T a, T b) { return a/b + !!(a%b); }
 
template<typename T> vector<T> make_v(size_t a) { return vector<T>(a); }
template<typename T,typename... Ts>
auto make_v(size_t a,Ts... ts) { 
  return vector<decltype(make_v<T>(ts...))>(a,make_v<T>(ts...));
}
template<typename T,typename V> typename enable_if<is_class<T>::value==0>::type
fill_v(T &t, const V &v) { t=v; }
template<typename T,typename V> typename enable_if<is_class<T>::value!=0>::type
fill_v(T &t, const V &v ) { for(auto &e:t) fill_v(e,v); }
 
template<class S,class T>
ostream &operator <<(ostream& out,const pair<S,T>& a){
  out<<'('<<a.first<<','<<a.second<<')'; return out;
}
template<typename T>
istream& operator >> (istream& is, vector<T>& vec){
  for(T& x: vec) {is >> x;} return is;
}
template<class T>
ostream &operator <<(ostream& out,const vector<T>& a){
  out<<'['; for(T i: a) {out<<i<<',';} out<<']'; return out;
}
 
int dx[] = {0, 1, 0, -1}, dy[] = {1, 0, -1, 0}; // DRUL
const int INF = 1<<30;
const ll LLINF = 1LL<<40;
const ll MOD = 1000000007;

signed main(void)
{
  cin.tie(0);
  ios::sync_with_stdio(false);

  double EPS = 1e-6;

  ll a, b, c;
  ll sx, sy, gx, gy;
  cin >> a >> b >> c;
  cin >> sx >> sy >> gx >> gy;

  auto dist = [](double x1, double y1, double x2, double y2) -> double {
    return sqrt((x1-x2)*(x1-x2) + (y1-y2)*(y1-y2));
  };
  auto getx = [&](double y) {
    return make_pair(-y*b/a-(double)c/a, y);
  };
  auto gety = [&](double x) {
    return make_pair(x, -x*a/b-(double)c/b);
  };

  vector<pair<double,double>> s, g;
  s.push_back(getx(sy));
  s.push_back(gety(sx));
  g.push_back(getx(gy));
  g.push_back(gety(gx));

  double ans = abs(sx-gx) + abs(sy-gy);
  for(auto p1: s) for(auto p2: g) {
    double tmp = dist(sx, sy, p1.first, p1.second);
    tmp += dist(p1.first, p1.second, p2.first, p2.second);
    tmp += dist(p2.first, p2.second, gx, gy);
    chmin(ans, tmp);
  }
  cout << fixed << setprecision(15) << ans << endl;

  return 0;
}

Educational Codeforces Round 54 D. Edge Deletion

Codeforces 競技プログラミング

問題ページ

考えたこと

  • 最短路DAGを考えると無向グラフで最短路に使われる辺だけを抽出すると木になるはず
  • dijkstraの途中で遷移に使った辺を覚えておけば最短路に使われる辺はわかる
  • k>=n-1であれば使われた辺すべてを出力すればよい
  • k<n-1であれば頂点1に連結になるような辺をk本選べばよい
  • 最短経路長が短い頂点の遷移に使った辺から取っていけば非連結な辺を取ることはないはず
  • 最短路に使う辺を列挙して最短経路長が短いものからmin(n-1,k)本の辺を取ればよさそう
#include <bits/stdc++.h>
 
using namespace std;
using ll = long long;
// #define int ll
using PII = pair<ll, ll>;
 
#define FOR(i, a, n) for (ll i = (ll)a; i < (ll)n; ++i)
#define REP(i, n) FOR(i, 0, n)
#define ALL(x) x.begin(), x.end()
 
template<typename T> T &chmin(T &a, const T &b) { return a = min(a, b); }
template<typename T> T &chmax(T &a, const T &b) { return a = max(a, b); }
template<typename T> bool IN(T a, T b, T x) { return a<=x&&x<b; }
template<typename T> T ceil(T a, T b) { return a/b + !!(a%b); }
 
template<typename T> vector<T> make_v(size_t a) { return vector<T>(a); }
template<typename T,typename... Ts>
auto make_v(size_t a,Ts... ts) { 
  return vector<decltype(make_v<T>(ts...))>(a,make_v<T>(ts...));
}
template<typename T,typename V> typename enable_if<is_class<T>::value==0>::type
fill_v(T &t, const V &v) { t=v; }
template<typename T,typename V> typename enable_if<is_class<T>::value!=0>::type
fill_v(T &t, const V &v ) { for(auto &e:t) fill_v(e,v); }
 
template<class S,class T>
ostream &operator <<(ostream& out,const pair<S,T>& a){
  out<<'('<<a.first<<','<<a.second<<')'; return out;
}
template<typename T>
istream& operator >> (istream& is, vector<T>& vec){
  for(T& x: vec) {is >> x;} return is;
}
template<class T>
ostream &operator <<(ostream& out,const vector<T>& a){
  out<<'['; for(T i: a) {out<<i<<',';} out<<']'; return out;
}
 
int dx[] = {0, 1, 0, -1}, dy[] = {1, 0, -1, 0}; // DRUL
const int INF = 1<<30;
const ll LLINF = 1LL<<60;
const ll MOD = 1000000007;

bool isprime[1000];

signed main(void)
{
  cin.tie(0);
  ios::sync_with_stdio(false);

  struct node {
    ll ver, cost, idx;
    node() {}
    node(ll a, ll b, ll c) : ver(a), cost(b), idx(c) {}
  };

  ll n, m, k;
  cin >> n >> m >> k;
  vector<vector<node>> g(n);
  REP(i, m) {
    ll a, b, c;
    cin >> a >> b >> c;
    a--, b--;
    g[a].push_back(node(b, c, i));
    g[b].push_back(node(a, c, i));
  }

  vector<PII> v(n);
  v[0] = {LLINF, -2};
  vector<ll> d(n, LLINF);
  d[0] = 0;
  priority_queue<PII, vector<PII>, greater<PII>> que;
  que.push({0, 0});
  while(que.size()) {
    PII p = que.top(); que.pop();
    if(d[p.second] < p.first) continue;
    for(auto to: g[p.second]) {
      if(d[to.ver] > d[p.second] + to.cost) {
        d[to.ver] = d[p.second] + to.cost;
        que.push({d[to.ver], to.ver});
        v[to.ver] = {d[to.ver], to.idx};
      }
    }
  }

  sort(ALL(v));
  cout << min(n-1, k) << endl;
  REP(i, min(n-1, k)) {
    cout << v[i].second+1 << " ";
  }
  cout << endl;

  return 0;
}