Educational Codeforces Round 1 F. Cut Length

問題ページ

直線上に多角形の頂点が存在しない場合、直線と辺の交点をに近い方から順番に見ていき、番目と番目の点の距離の和が答えになる。問題は直線上に多角形の頂点が存在する場合で、2つの辺と交わっていると判定されて困る。

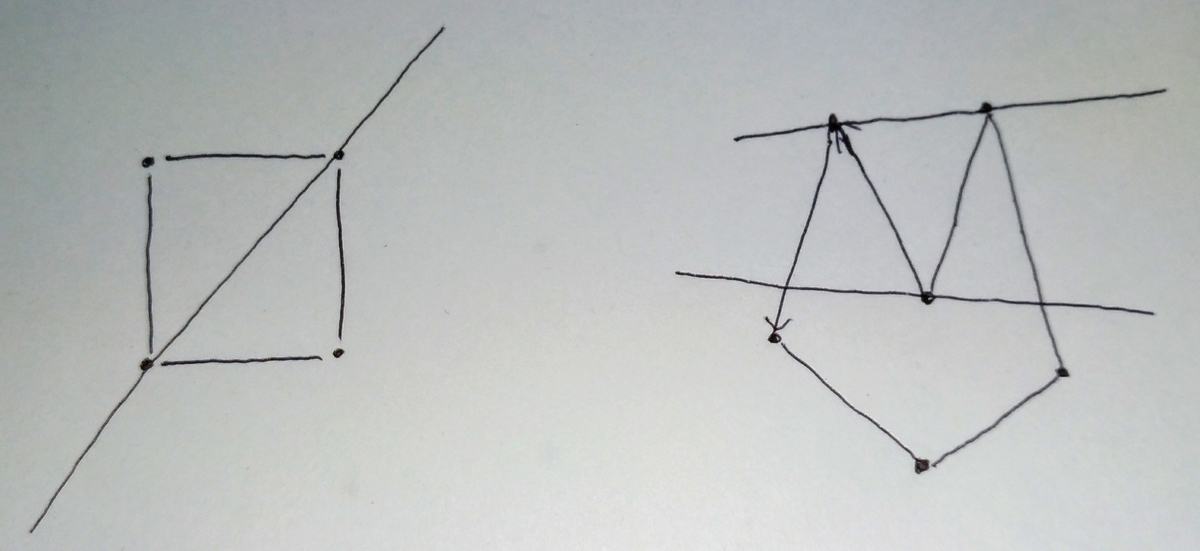点を通過して中に入るパターンだけではなく、点上を通過しても中に入らないパターンとか、内部で点を通過するだけなパターンとかいろいろある

これを解決するために多角形の中(=2)・点上(=1)・外(=0)の3状態に分ける。からに移動する過程で、各交点でどのように状態が変化するのか考える。多角形の頂点を予め反時計回りに並べておくことにする(与えられた多角形の符号付き面積を求め、負なら時計回りなのでreverseすればよい)と、線分 の左が中、直線上が点上、右が外となる。直線 から見て が左、点上、右のどれかに応じて、直線 と線分 の交点で状態がどう変化するか決定できる。

線分からある点がどこにあるか？はccw関数を用いて判定できるので、あとは実際に に近い交点から順に見ていき、状態が1以上であれば答えに距離を加算するとすればよい。

#include <bits/stdc++.h>  
using namespace std;  
using ll = long long;  
using PII = pair<ll, ll>;  
#define FOR(i, a, n) for (ll i = (ll)a; i < (ll)n; ++i)  
#define REP(i, n) FOR(i, 0, n)  
#define ALL(x) x.begin(), x.end()  
template<typename T> void chmin(T &a, const T &b) { a = min(a, b); }  
template<typename T> void chmax(T &a, const T &b) { a = max(a, b); }  
struct FastIO {FastIO() { cin.tie(0); ios::sync_with_stdio(0); }}fastiofastio;  
const ll INF = 1LL<<60;  
  
using R = long double; // Rにmint渡せるようにする  
using P = complex<R>;  
using L = pair<P,P>;  
using G = vector<P>;  
struct C {  
    P c; R r;  
    C() {}  
    C(const P &a, const R &b) : c(a), r(b) {}  
};  
struct S : public L {  
    S() {}  
    S(const P &a, const P &b) : L(a,b) {}  
};  
  
const R EPS = 1e-14;  
const R PI = atanl(1)*4;  
  
inline int sgn(const R& r) { return (r>EPS) - (r<-EPS); }  
inline R dot(const P& a, const P& b) {  
    return real(a)*real(b) + imag(a)*imag(b);  
}  
inline R det(const P& a, const P& b) {  
    return real(a)*imag(b) - imag(a)*real(b);  
}  
inline P vec(const L& l) {return l.second - l.first;}  
namespace std {  
    bool operator < (const P& a, const P& b) {  
        return sgn(real(a-b)) ? real(a-b) < 0 : sgn(imag(a-b)) < 0;  
    }  
    bool operator == (const P& a, const P& b) {  
        return sgn(real(a-b)) == 0 && sgn(imag(a-b)) == 0;  
    }  
}  
  
inline istream& operator>>(istream& is, P& p) {  
    R x, y;  
    is >> x >> y;  
    p = P(x, y);  
    return is;  
}  
  
// 線分abから見たcの位置  
enum CCW{LEFT=1, RIGHT=2, BACK=4, FRONT=8, ON_SEG=16};  
int ccw(P a, P b, P c) {  
    P p = (c-a)/(b-a);  
    if(sgn(imag(p)) > 0) return LEFT;  
    if(sgn(imag(p)) < 0) return RIGHT;  
    if(sgn(real(p)) < 0) return BACK;  
    if(sgn(real(p)-1) > 0) return FRONT;  
    return ON_SEG;  
}  
  
// 交点 交差判定を先にすること!!!  
inline P crosspoint(const L& l1, const L& l2) {  
    R ratio = det(vec(l2), l2.first-l1.first)/det(vec(l2),vec(l1));  
    return l1.first + vec(l1)*ratio;  
}  
  
// 面積 頂点が反時計回りに並んでいること  
R area(const G& pol) {  
    R ret = 0.0;  
    REP(i, pol.size()) ret += det(pol[i], pol[(i+1)%pol.size()]);  
    return (ret/2.0);  
}  
  
int main(void) {  
    ll n, m;  
    cin >> n >> m;  
    vector<P> ps(n);  
    REP(i, n) cin >> ps[i];  
    if(sgn(area(ps)) < 0) reverse(ALL(ps));  
  
    REP(i, m) {  
        P a, b;  
        cin >> a >> b;  
        if(b < a) swap(a, b);  
  
        vector<pair<P, ll>> v;  
        REP(i, n) {  
            auto type1 = ccw(a, b, ps[i]), type2 = ccw(a, b, ps[(i+1)%n]);  
            if(type1==BACK || type1==FRONT) type1 = ON_SEG;  
            if(type2==BACK || type2==FRONT) type2 = ON_SEG;  
            // そもそも交差してない or 直線が線分を含む  
            if(type1 == type2) continue;  
  
            ll diff;  
            if(type1==RIGHT && type2==LEFT) diff = -2;  
            else if(type1==RIGHT && type2==ON_SEG) diff = -1;  
            else if(type1==LEFT && type2==RIGHT) diff = 2;  
            else if(type1==LEFT && type2==ON_SEG) diff = 1;  
            else if(type1==ON_SEG && type2==RIGHT) diff = 1;  
            else if(type1==ON_SEG && type2==LEFT) diff = -1;  
  
            auto cp = crosspoint(L(a, b), L(ps[i], ps[(i+1)%n]));  
            v.push_back({cp, diff});  
        }  
        sort(ALL(v));  
  
        ll sum = v.size() ? v[0].second : 0;  
        R ans = 0;  
        FOR(i, 1, v.size()) {  
            if(sum > 0) ans += abs(v[i].first - v[i-1].first);  
            sum += v[i].second;  
        }  
        cout << fixed << setprecision(9) << ans << "\n";  
    }  
  
    return 0;  
}