ARC084 E - Finite Encyclopedia of Integer Sequences

問題ページ

解法

まずKが偶数ならば(K/2, K, …, K)となる数列が答えになることがわかる。よってKが奇数のものについてのみ考える。
ナイーブな解法として答えの数列でi番目で数列のa番目をつくるにはi番目の数字が一意に定まるとして前から決めていくような解法がある。しかしk,nに大きな値がきたときにaの値がまともに持てるような大きさの値ではなくなってしまう。したがって何か別の小さい値を利用して答えを求める必要がある。X/2番目の数列に近そうな数列として ceil(K/2) を並べるものがある。この数列と答えとなる数列が何個ずれているか？というずれであればあまり大きい値ではなさそう。このずれがどの程度の大きさなのか実験してみる。

k=3での実験

実験結果を見ると答えの数列はceil(K/2)を並べた数列とn/2ずれていることがわかる。数列を辞書順で一つ前のものに戻す操作はならしO(1)で可能なので全体でO(N)で解ける。

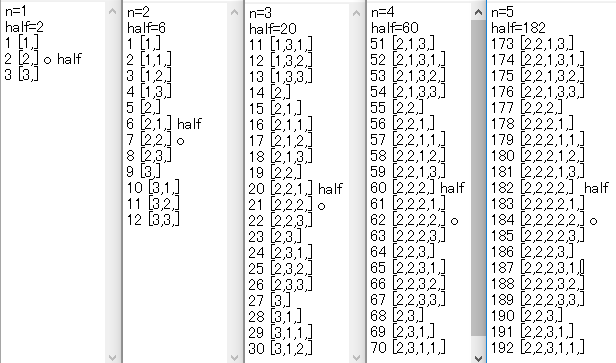
実験難しい…
ならしO(1)で戻す処理の雰囲気にAGC029 C - Lexicographic constraintsを感じた

#include <bits/stdc++.h>

using namespace std;
using ll = long long;
// #define int ll
using PII = pair<ll, ll>;

#define FOR(i, a, n) for (ll i = (ll)a; i < (ll)n; ++i)
#define REP(i, n) FOR(i, 0, n)
#define ALL(x) x.begin(), x.end()

template<typename T> T &chmin(T &a, const T &b) { return a = min(a, b); }
template<typename T> T &chmax(T &a, const T &b) { return a = max(a, b); }
template<typename T> bool IN(T a, T b, T x) { return a<=x&&x<b; }
template<typename T> T ceil(T a, T b) { return a/b + !!(a%b); }

template<typename T> vector<T> make_v(size_t a) { return vector<T>(a); }
template<typename T,typename... Ts>
auto make_v(size_t a,Ts... ts) {
  return vector<decltype(make_v<T>(ts...))>(a,make_v<T>(ts...));
}
template<typename T,typename V> typename enable_if<is_class<T>::value==0>::type
fill_v(T &t, const V &v) { t=v; }
template<typename T,typename V> typename enable_if<is_class<T>::value!=0>::type
fill_v(T &t, const V &v ) { for(auto &e:t) fill_v(e,v); }

template<class S,class T>
ostream &operator <<(ostream& out,const pair<S,T>& a){
  out<<'('<<a.first<<','<<a.second<<')'; return out;
}
template<typename T>
istream& operator >> (istream& is, vector<T>& vec){
  for(T& x: vec) {is >> x;} return is;
}
template<class T>
ostream &operator <<(ostream& out,const vector<T>& a){
  out<<'['; for(T i: a) {out<<i<<',';} out<<']'; return out;
}

int dx[] = {0, 1, 0, -1}, dy[] = {1, 0, -1, 0}; // DRUL
const int INF = 1<<30;
const ll LLINF = 1LL<<60;
const ll MOD = 1000000007;

// 実験
//int n = 5, k = 3;
//vector<vector<ll>> a;
//
//void dfs(vector<ll> v) {
//  if(v.size()) a.push_back(v);
//  if(v.size() == n) return;
//
//  REP(i, k) {
//    vector<ll> u(v);
//    u.push_back(i+1);
//    dfs(u);
//  }
//}

signed main(void)
{
  cin.tie(0);
  ios::sync_with_stdio(false);

  // 実験
//  dfs({});
//  sort(ALL(a));
//  ll half = ceil((int)a.size(), 2);
//  cout << "half=" << half << endl;
//  for(int i=max(half-10, 0LL); i<min(half+10, (ll)a.size()); ++i) {
//    cout << i+1 << " " << a[i] << endl;
//  }
//
//  return 0;

  ll n, k;
  cin >> k >> n;

  if(k%2 == 0) {
    cout << k/2;
    REP(i, n-1) cout << " " << k;
    cout << endl;
    return 0;
  }

  vector<ll> ans(n, ceil(k, 2LL));
  REP(i, n/2) {
    if(ans.back() == 1) ans.pop_back();
    else {
      ans[ans.size()-1]--;
      while(ans.size() != n) ans.push_back(k);
    }
  }

  REP(i, ans.size()) cout << ans[i] << " ";
  cout << endl;

  return 0;
}