SRM673 div1 easy BearCavalry

考えたこと

• とりあえずソートしない理由はなさそう
• 明らかに二部マッチング
• 完全二部マッチングの個数の数え上げ
• NPなので無理です
• ソートしてあるとwarriors[i]とマッチングできるhorse[j]についてjの区間は[0,x]になって単調増加する
• warriors[i]がマッチングできる馬の範囲について適当に図を書いてみる
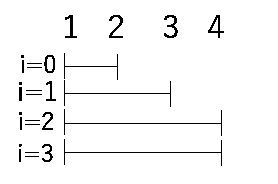
• 単調増加してるから前のwarriorsについて選んだ馬は区間に含まれているはず
• なので(i番目の区間の幅)-iを掛ければいいだけ
• 出すと通る

#include <bits/stdc++.h>

using namespace std;
using ll = long long;
using VI = vector<int>;
using VVI = vector<VI>;
using PII = pair<int, int>;

#define FOR(i, a, n) for (ll i = (ll)a; i < (ll)n; ++i)
#define REP(i, n) FOR(i, 0, n)
#define ALL(x) x.begin(), x.end()
#define PB push_back

const ll LLINF = (1LL<<60);
const int INF = (1LL<<30);
const int MOD = 1000000007;

template <typename T> T &chmin(T &a, const T &b) { return a = min(a, b); }
template <typename T> T &chmax(T &a, const T &b) { return a = max(a, b); }
template <typename T> bool IN(T a, T b, T x) { return a<=x&&x<b; }
template<typename T> T ceil(T a, T b) { return a/b + !!(a%b); }
template<class S,class T>
ostream &operator <<(ostream& out,const pair<S,T>& a){
  out<<'('<<a.first<<','<<a.second<<')';
  return out;
}
template<class T>
ostream &operator <<(ostream& out,const vector<T>& a){
  out<<'[';
  REP(i, a.size()) {out<<a[i];if(i!=a.size()-1)out<<',';}
  out<<']';
  return out;
}

int dx[] = {0, 1, 0, -1}, dy[] = {1, 0, -1, 0};

// ll

class BearCavalry {
   public:
   int countAssignments(vector <int> warriors, vector <int> horses)
  {
    ll n = warriors.size();
    ll best = warriors[0];
    warriors.erase(warriors.begin());
    sort(ALL(warriors)); reverse(ALL(warriors));
    sort(ALL(horses));

    ll ans = 0;
    // horses[i] を 0に割り当て
    REP(i, n) {
      // warriors[j] * horses[x] が best * horses[i] を超えない最大のx
      ll ret = 1;
      bool flag = true;
      REP(j, n-1) {
        ll idx = 0;
        REP(x, n) {
          if(x == i) continue;
          if(warriors[j] * horses[x] >= best * horses[i]) break;
          idx++;
        }
        if(idx-j <= 0) {
          flag = false;
          break;
        }
        (ret *= (idx-j)) %= MOD;
      }
      if(flag) (ans += ret) %= MOD;
    }

    return ans;
  }
};