ferinの競プロ帳

競プロについてのメモ

AtCoder Beginner Contest 164 F - I hate Matrix Construction

AtCoder

問題ページ

ビットごとに独立

ビットごとの論理和・論理積について考えているため、ビットごとに独立に考えることができる。したがって要素が0か1の N \times N の行列を構築できるか？の問題に帰着できた。

容易に決定できる要素

まず、0か1か確定させられる要素を決めてしまおう。

  • 論理積が1の行/列：全て1
  • 論理和が0の行/列：全て0
  • s_y=t_x であるような (y,x)：s_y

残りの要素

残りの決まっていない要素は「論理積が0」と「論理和が1」の制約からなる要素だけである。

試しにこれらの要素を全て0としてみる。このとき「論理積が0」という制約に反することはない。「論理和が1」が満たされない場合の対処を考える。そのような行(列)が存在する場合、「論理積が0」である列(行)のいずれかの要素を1にする必要がある。「論理積が0」である列(行)の要素を1にしたときに、その列(行)の要素が全て1にならないのであれば、1にしても問題がない。この条件を満たす列(行)を探し、1に変更する処理を「論理和が1」が満たされない全ての行(列)に対して行う。

行列の存在性

この処理を行った結果の行列が制約を満たさないならば、答えは-1である。結果が条件を満たさない場合、矛盾するパターンは2通り存在する。いずれの場合でも行列が存在することはありえない。

  • 「容易に決定できる要素」の分で矛盾
    「論理積が1」から1にしたいが「論理和が0」から0にする必要があるので不可能である。
or 0 or 0
and 1 無理 無理
  • 「残りの要素」の分で矛盾
    0→1に変更する要素が足りないので「論理和が1」の制約を修正することは不可能である。

実装に関して

a_{i,j} \lt 2^{64} より要素はunsigned long long intで管理する必要がある。また1<<iではなく1ULL<<iとしなければいけない。

#include <bits/stdc++.h>  
using namespace std;  
using ll = unsigned long long int;  
using PII = pair<ll, ll>;  
#define FOR(i, a, n) for(ll i=(ll)a; i<(ll)n; ++i)  
#define REP(i, n) FOR(i, 0, n)  
#define ALL(x) x.begin(), x.end()  
template<typename T> void chmin(T &a, const T &b) { a = min(a, b); }  
template<typename T> void chmax(T &a, const T &b) { a = max(a, b); }  
struct FastIO {FastIO() { cin.tie(0); ios::sync_with_stdio(0); }}fastiofastio;  
#ifdef DEBUG  
#include "../program_contest_library/memo/dump.hpp"  
#else  
#define dump(...)  
#endif  
constexpr ll INF = 1ULL<<60;  
  
int main() {  
    ll n;  
    cin >> n;  
    // 0 → and, 1 → or  
    vector<ll> s(n), t(n), u(n), v(n);  
    REP(i, n) cin >> s[i];  
    REP(i, n) cin >> t[i];  
    REP(i, n) cin >> u[i];  
    REP(i, n) cin >> v[i];  
  
    vector<vector<ll>> ans(n, vector<ll>(n));  
    REP(i, 64) {  
        // u2[j] = u[j]のiビット目  
        vector<ll> u2(n), v2(n);  
        REP(j, n) u2[j] = !!(u[j]&1ULL<<i), v2[j] = !!(v[j]&1ULL<<i);  
          
        // 確定させられる要素の分を決定  
        vector<vector<ll>> used(n, vector<ll>(n));  
        REP(j, n) if(s[j]==0 && u2[j]==1) REP(k, n) used[j][k] = 1;  
        REP(j, n) if(t[j]==0 && v2[j]==1) REP(k, n) used[k][j] = 1;  
        REP(j, n) REP(k, n) if(u2[j] == v2[k]) used[j][k] = u2[j];  
  
        // 論理和が1の行の制約を満たせるように  
        {  
            vector<ll> zeros(n);  
            REP(j, n) REP(k, n) zeros[k] += (used[j][k]==0);  
            REP(j, n) if(s[j]==1 && u2[j]==1) {  
                bool exist = false;  
                REP(k, n) if(used[j][k]==1) exist = true;  
                if(exist) continue;  
                // 制約違反の行がある  
                //「論理積が0」で1に変更しても0が残っている列を探す  
                REP(k, n) if(t[k]==0 && v2[k]==0 && zeros[k]>=2) {  
                    zeros[k]--;  
                    used[j][k] = 1;  
                    break;  
                }  
            }  
        }  
        // 論理和が1の列の制約を満たすように  
        {  
            vector<ll> zeros(n);  
            REP(j, n) REP(k, n) zeros[j] += (used[j][k]==0);  
            REP(j, n) if(t[j]==1 && v2[j]==1) {  
                bool exist = false;  
                REP(k, n) if(used[k][j]==1) exist = true;  
                if(exist) continue;  
                REP(k, n) if(s[k]==0 && u2[k]==0 && zeros[k]>=2) {  
                    zeros[k]--;  
                    used[k][j] = 1;  
                    break;  
                }  
            }  
        }  
          
        REP(j, n) REP(k, n) ans[j][k] |= used[j][k]<<i;  
    }  
  
    // 実際に構成した行列が制約を満たすか確認  
    auto check = [&] {  
        REP(i, n) {   
            ll and1 = ans[i][0], or1 = 0, and2 = ans[0][i], or2 = 0;  
            REP(j, n) {  
                and1 &= ans[i][j];  
                or1  |= ans[i][j];  
                and2 &= ans[j][i];  
                or2  |= ans[j][i];  
            }  
            if(s[i]==0 && u[i]!=and1) return false;  
            if(s[i]==1 && u[i]!=or1) return false;  
            if(t[i]==0 && v[i]!=and2) return false;  
            if(t[i]==1 && v[i]!=or2) return false;  
        }  
        return true;  
    };  
    if(!check()) {  
        cout << -1 << endl;  
        return 0;  
    }  
  
    REP(i, n) REP(j, n) cout << ans[i][j] << (j==n-1?'\n':' ');  
  
    return 0;  
}

Code Formula 2014 本選 E - ab文字列

AtCoder

問題ページ

文字列の長さは n についてフィボナッチ数列になっている。したがって n については一意に定まる。また、フィボナッチ数列で20000以下となるのは22番目までなので、n \leq 22 である。文字列は高々 2^{20} 個程度しか存在しないので、F_{n,k}\ (0 \leq k \lt 2^{n-2} \leq 2^{20}) を全列挙し、S と一致するか判定すればよい。

普通に文字列の一致判定に O(|S|) かけているとTLEするのでハッシュを用いて高速化する。ローリングハッシュの要領でハッシュ関数を定めると、文字列 sl, sr を連結した文字列の sl+sr のハッシュは高速に求められる。f(n,k) の値をメモ化再帰で計算していくことで O(n2^n) で F_{n,k} のハッシュを求められる。

MLには注意

#include <bits/stdc++.h>  
using namespace std;  
using ll = long long;  
using PII = pair<ll, ll>;  
#define FOR(i, a, n) for(ll i=(ll)a; i<(ll)n; ++i)  
#define REP(i, n) FOR(i, 0, n)  
#define ALL(x) x.begin(), x.end()  
template<typename T> void chmin(T &a, const T &b) { a = min(a, b); }  
template<typename T> void chmax(T &a, const T &b) { a = max(a, b); }  
struct FastIO {FastIO() { cin.tie(0); ios::sync_with_stdio(0); }}fastiofastio;  
#ifdef DEBUG  
#include "../program_contest_library/memo/dump.hpp"  
#else  
#define dump(...)  
#endif  
constexpr ll INF = 1LL<<60;  
  
struct dice {  
    mt19937 mt;  
    dice() : mt(chrono::steady_clock::now().time_since_epoch().count()) {}  
    ll operator()(ll x) { return this->operator()(0, x - 1); }  
    ll operator()(ll x, ll y) {  
        uniform_int_distribution<ll> dist(x, y);  
        return dist(mt);  
    }  
} rnd;  
  
class rollingHash {  
private:  
    static constexpr ll mod = (1LL<<61) - 1;  
    const ll base;  
    vector<ll> hash, p;  
  
    ll mul(ll a, ll b) {  
        ll au = a>>31, ad = a & ((1LL<<31)-1);  
        ll bu = b>>31, bd = b & ((1LL<<31)-1);  
        ll mid = ad*bu+au*bd, midu = mid>>30, midd = mid & ((1LL<<30)-1);  
        return au*bu*2 + midu + (midd<<31) + ad*bd;  
    }  
    ll calcmod(ll x) {  
        ll ret = (x>>61) + (x & mod);  
        if(ret >= mod) ret -= mod;  
        return ret;  
    }  
  
public:  
    rollingHash(const string &s) : base(rnd(2, 100000)), hash(s.size()+1), p(s.size()+1,1) {  
        REP(i, s.size()) {  
            hash[i+1] = calcmod(mul(hash[i], base)+s[i]);  
            p[i+1] = calcmod(mul(p[i], base));  
        }  
    }  
    // [l,r)  
    ll get(int l,int r) {  
        return calcmod(hash[r] + 3*mod - mul(hash[l], p[r-l]));  
    }  
    ll concat(ll h1, ll h2, ll h2len) {  
        return calcmod(mul(h1, p[h2len]) + h2);  
    }  
};  
  
int main() {  
    string s;  
    cin >> s;  
      
    if(s.size()==1) {  
        if(s=="a") cout << "2 0\n";  
        else cout << "1 0\n";  
        return 0;  
    }  
  
    rollingHash hash(s);  
    ll ha = -1, hb = -1;  
    REP(i, s.size()) {  
        if(s[i]=='a') ha = hash.get(i, i+1);  
        else if(s[i]=='b') hb = hash.get(i, i+1);  
    }  
    ll hs = hash.get(0, s.size());  
  
    // fib[i] = (f_{ij}の長さ)  
    vector<ll> fib({0, 1, 1, 2});  
    {  
        ll a = 1, b = 1, c = 2;  
        while(c < (ll)s.size()) {  
            a = b;  
            b = c;  
            c = a+b;  
            fib.push_back(c);  
        }  
    }  
    ll n = fib.size()-1;  
  
    vector<vector<ll>> memo(n+1);  
    FOR(i, 3, n+1) memo[i].assign(1LL<<(i-2), -1);  
    auto dfs = [&](auto &&self, ll x, ll y) -> ll {  
        if(x==1) return hb;  
        if(x==2) return ha;  
        if(memo[x][y] != -1) return memo[x][y];  
        if(y%2==0) {  
            auto vl = self(self, x-1, y/2);  
            auto vr = self(self, x-2, y/4);  
            return memo[x][y] = hash.concat(vl, vr, fib[x-2]);  
        } else {  
            auto vl = self(self, x-2, y/4);  
            auto vr = self(self, x-1, y/2);  
            return memo[x][y] = hash.concat(vl, vr, fib[x-1]);  
        }  
    };  
  
    REP(i, 1LL<<(n-2)) if(dfs(dfs, n, i) == hs) {  
        cout << n << " " << i << "\n";  
        return 0;  
    }  
  
    return 0;  
}

Educational Codeforces Round 3 F. Frogs and mosquitoes

codeforces

問題ページ
flogに対応する区間を持つ集合・まだ食べられていないmosquitoを保持する集合をそれぞれ保持しておく。

mosquito (p, b) が現れたとする。このとき p を含む区間が存在するか？存在するなら左端が最も小さいものはどれか？を判定したい。内包される区間に対応するflogが新たにmosquitoを食べることはない。内包される区間は削除しておくことにすると、p を含みうる区間は一通りに定まり、二分探索で求められる。

p を含む区間の右端を b 伸ばす。flogの集合のうち、内包されるようになった区間を削除しておく。削除される回数は高々1回なので計算量は問題ない。まだ食べられていないmosquitoのうち、左にいる方から順に、伸びた区間に含まれるか？を判定して伸ばす処理を行う。

#include <bits/stdc++.h>  
using namespace std;  
using ll = long long;  
using PII = pair<ll, ll>;  
#define FOR(i, a, n) for (ll i = (ll)a; i < (ll)n; ++i)  
#define REP(i, n) FOR(i, 0, n)  
#define ALL(x) x.begin(), x.end()  
template<typename T> void chmin(T &a, const T &b) { a = min(a, b); }  
template<typename T> void chmax(T &a, const T &b) { a = max(a, b); }  
struct FastIO {FastIO() { cin.tie(0); ios::sync_with_stdio(0); }}fastiofastio;  
#ifdef DEBUG_   
#include "../program_contest_library/memo/dump.hpp"  
#else  
#define dump(...)  
#endif  
const ll INF = 1LL<<60;  
  
int main(void) {  
    ll n, m;  
    cin >> n >> m;  
    vector<ll> x(n), t(n), p(m), b(m);  
    REP(i, n) cin >> x[i] >> t[i];  
    REP(i, m) cin >> p[i] >> b[i];  
  
    set<PII> flog;  
    {  
        vector<ll> ord(n);  
        iota(ALL(ord), 0);  
        sort(ALL(ord), [&](ll l, ll r){  
            return PII(x[l], x[l]+t[l]) < PII(x[r], x[r]+t[r]);  
        });  
        for(auto i: ord) {  
            // 内包されるならスルー  
            if(flog.size() && x[i]+t[i] <= flog.rbegin()->first) continue;  
            flog.insert({x[i]+t[i], i});  
        }  
    }  
  
    vector<ll> cnt(n);  
    // 区間idxをlen長くする  
    auto extend = [&](ll idx, ll len) {  
        flog.erase({x[idx]+t[idx], idx});  
        while(1) {  
            // r <= x[idx]+t[idx]+len の区間を消す  
            auto itr = flog.lower_bound({x[idx]+t[idx], 0});  
            if(itr != flog.end() && itr->first <= x[idx]+t[idx]+len) flog.erase(itr);  
            else break;  
        }  
        cnt[idx]++;  
        t[idx] += len;  
        flog.insert({x[idx]+t[idx], idx});  
    };  
  
    multiset<PII> rest;  
    REP(i, m) {  
        auto itr = flog.lower_bound({p[i], 0});  
        if(itr != flog.end() && x[itr->second] <= p[i]) {  
            ll idx = itr->second;  
            extend(idx, b[i]);  
  
            while(1) {  
                auto ritr = rest.lower_bound({x[idx], 0});  
                if(ritr!=rest.end() && ritr->first <= x[idx]+t[idx]) {  
                    extend(idx, ritr->second);  
                    rest.erase(ritr);  
                } else {  
                    break;  
                }  
            }  
        } else {  
            rest.insert({p[i], b[i]});  
        }  
    }  
  
    REP(i, n) cout << cnt[i] << " " << t[i] << "\n";  
  
    return 0;  
}

setとmultisetを間違えて1時間半溶かしました

Educational Codeforces Round 1 F. Cut Length

codeforces

問題ページ

直線ab上に多角形の頂点\{p_i\}_{i=0}^{n-1}が存在しない場合、直線と辺の交点をaに近い方から順番に見ていき、2i番目と2i+1番目の点の距離の和が答えになる。問題は直線上に多角形の頂点が存在する場合で、2つの辺と交わっていると判定されて困る。

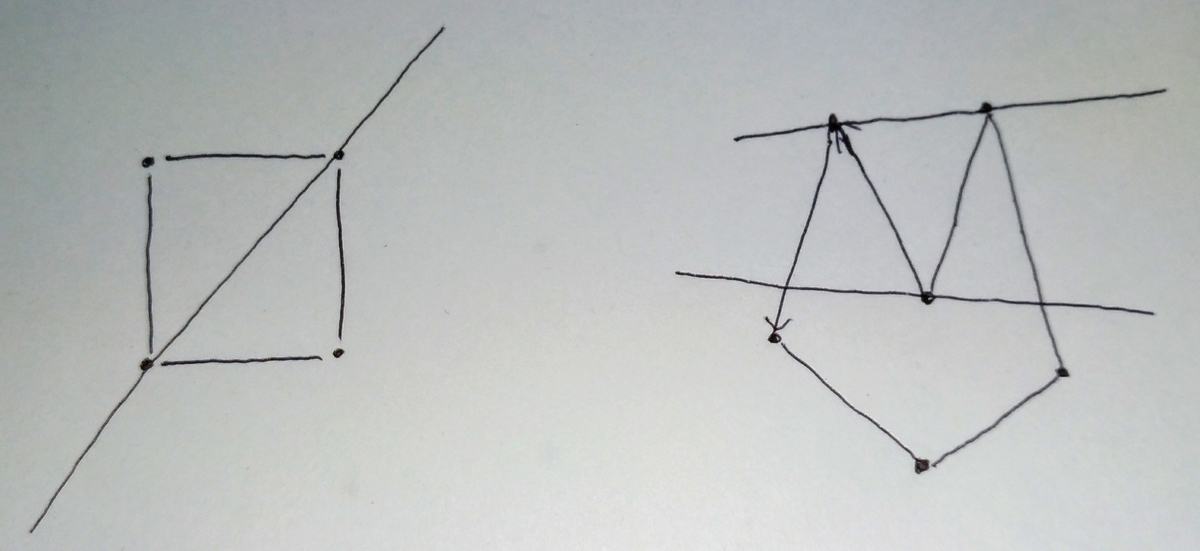f:id:ferin_tech:20200407210655j:plain 点を通過して中に入るパターンだけではなく、点上を通過しても中に入らないパターンとか、内部で点を通過するだけなパターンとかいろいろある

これを解決するために多角形の中(=2)・点上(=1)・外(=0)の3状態に分ける。aからbに移動する過程で、各交点でどのように状態が変化するのか考える。多角形の頂点を予め反時計回りに並べておくことにする(与えられた多角形の符号付き面積を求め、負なら時計回りなのでreverseすればよい)と、線分 p_{i}, p_{i+1} の左が中、直線上が点上、右が外となる。直線 ab から見て p_i, p_{i+1} が左、点上、右のどれかに応じて、直線 ab と線分 p_i, p_{i+1} の交点で状態がどう変化するか決定できる。

線分からある点がどこにあるか？はccw関数を用いて判定できるので、あとは実際に a に近い交点から順に見ていき、状態が1以上であれば答えに距離を加算するとすればよい。

#include <bits/stdc++.h>  
using namespace std;  
using ll = long long;  
using PII = pair<ll, ll>;  
#define FOR(i, a, n) for (ll i = (ll)a; i < (ll)n; ++i)  
#define REP(i, n) FOR(i, 0, n)  
#define ALL(x) x.begin(), x.end()  
template<typename T> void chmin(T &a, const T &b) { a = min(a, b); }  
template<typename T> void chmax(T &a, const T &b) { a = max(a, b); }  
struct FastIO {FastIO() { cin.tie(0); ios::sync_with_stdio(0); }}fastiofastio;  
const ll INF = 1LL<<60;  
  
using R = long double; // Rにmint渡せるようにする  
using P = complex<R>;  
using L = pair<P,P>;  
using G = vector<P>;  
struct C {  
    P c; R r;  
    C() {}  
    C(const P &a, const R &b) : c(a), r(b) {}  
};  
struct S : public L {  
    S() {}  
    S(const P &a, const P &b) : L(a,b) {}  
};  
  
const R EPS = 1e-14;  
const R PI = atanl(1)*4;  
  
inline int sgn(const R& r) { return (r>EPS) - (r<-EPS); }  
inline R dot(const P& a, const P& b) {  
    return real(a)*real(b) + imag(a)*imag(b);  
}  
inline R det(const P& a, const P& b) {  
    return real(a)*imag(b) - imag(a)*real(b);  
}  
inline P vec(const L& l) {return l.second - l.first;}  
namespace std {  
    bool operator < (const P& a, const P& b) {  
        return sgn(real(a-b)) ? real(a-b) < 0 : sgn(imag(a-b)) < 0;  
    }  
    bool operator == (const P& a, const P& b) {  
        return sgn(real(a-b)) == 0 && sgn(imag(a-b)) == 0;  
    }  
}  
  
inline istream& operator>>(istream& is, P& p) {  
    R x, y;  
    is >> x >> y;  
    p = P(x, y);  
    return is;  
}  
  
// 線分abから見たcの位置  
enum CCW{LEFT=1, RIGHT=2, BACK=4, FRONT=8, ON_SEG=16};  
int ccw(P a, P b, P c) {  
    P p = (c-a)/(b-a);  
    if(sgn(imag(p)) > 0) return LEFT;  
    if(sgn(imag(p)) < 0) return RIGHT;  
    if(sgn(real(p)) < 0) return BACK;  
    if(sgn(real(p)-1) > 0) return FRONT;  
    return ON_SEG;  
}  
  
// 交点 交差判定を先にすること!!!  
inline P crosspoint(const L& l1, const L& l2) {  
    R ratio = det(vec(l2), l2.first-l1.first)/det(vec(l2),vec(l1));  
    return l1.first + vec(l1)*ratio;  
}  
  
// 面積 頂点が反時計回りに並んでいること  
R area(const G& pol) {  
    R ret = 0.0;  
    REP(i, pol.size()) ret += det(pol[i], pol[(i+1)%pol.size()]);  
    return (ret/2.0);  
}  
  
int main(void) {  
    ll n, m;  
    cin >> n >> m;  
    vector<P> ps(n);  
    REP(i, n) cin >> ps[i];  
    if(sgn(area(ps)) < 0) reverse(ALL(ps));  
  
    REP(i, m) {  
        P a, b;  
        cin >> a >> b;  
        if(b < a) swap(a, b);  
  
        vector<pair<P, ll>> v;  
        REP(i, n) {  
            auto type1 = ccw(a, b, ps[i]), type2 = ccw(a, b, ps[(i+1)%n]);  
            if(type1==BACK || type1==FRONT) type1 = ON_SEG;  
            if(type2==BACK || type2==FRONT) type2 = ON_SEG;  
            // そもそも交差してない or 直線が線分を含む  
            if(type1 == type2) continue;  
  
            ll diff;  
            if(type1==RIGHT && type2==LEFT) diff = -2;  
            else if(type1==RIGHT && type2==ON_SEG) diff = -1;  
            else if(type1==LEFT && type2==RIGHT) diff = 2;  
            else if(type1==LEFT && type2==ON_SEG) diff = 1;  
            else if(type1==ON_SEG && type2==RIGHT) diff = 1;  
            else if(type1==ON_SEG && type2==LEFT) diff = -1;  
  
            auto cp = crosspoint(L(a, b), L(ps[i], ps[(i+1)%n]));  
            v.push_back({cp, diff});  
        }  
        sort(ALL(v));  
  
        ll sum = v.size() ? v[0].second : 0;  
        R ans = 0;  
        FOR(i, 1, v.size()) {  
            if(sum > 0) ans += abs(v[i].first - v[i-1].first);  
            sum += v[i].second;  
        }  
        cout << fixed << setprecision(9) << ans << "\n";  
    }  
  
    return 0;  
}

Educational Codeforces Round 2 D. Area of Two Circles' Intersection

codeforces

問題ページ

まず2円が離れているか外接の関係にある場合、答えは0です。2円が内包か内接の関係にある場合、答えは \pi \min(r_1, r_2)^2 です。2円が2点で交差する場合について、2通りに場合分けを行います。

  • 交点からなる線分から見て、(x_1,y_1),(x_2,y_2) が反対側にある
    扇形ABCから三角形ABCを引くことで、各円について斜線部の領域を求めます。斜線部の和が答えの面積になります。 f:id:ferin_tech:20200315220846p:plainf:id:ferin_tech:20200315220850p:plain
  • 交点からなる線分から見て、(x_1,y_1),(x_2,y_2) が同じ側にある
    半径が大きい方の円については先程と同様に、扇形から三角形を引きます。半径が小さい方については扇形の面積に三角形を"足す"ことで該当する領域の面積を求められます。
    f:id:ferin_tech:20200315220857p:plainf:id:ferin_tech:20200315220906p:plain

どちらかの円の中心が交点からなる線分上に乗っている場合もありますが、その場合足し引きする三角形の面積が0なのでどちらでも大丈夫です。どちらの場合にあたるか？を調べるにはccw関数などを用いればよいです。

扇形と三角形の面積を求めます。扇形については r^2 \angle BAC / 2、三角形については r^2 \sin \angle BAC / 2 で求められます。角度については内積を求める式 \vec{a} \cdot \vec{b} = |\vec{a}||\vec{b}|\cos \angle BAC より \angle BAC = \arccos (\vec{a} \cdot \vec{b}) / |\vec{a}||\vec{b}| と求められます。

#include <bits/stdc++.h>  
using namespace std;  
using ll = long long;  
using PII = pair<ll, ll>;  
#define FOR(i, a, n) for (ll i = (ll)a; i < (ll)n; ++i)  
#define REP(i, n) FOR(i, 0, n)  
#define ALL(x) x.begin(), x.end()  
template<typename T> void chmin(T &a, const T &b) { a = min(a, b); }  
template<typename T> void chmax(T &a, const T &b) { a = max(a, b); }  
struct FastIO {FastIO() { cin.tie(0); ios::sync_with_stdio(0); }}fastiofastio;  
#ifdef DEBUG_   
#include "../program_contest_library/memo/dump.hpp"  
#else  
#define dump(...)  
#endif  
const ll INF = 1LL<<60;  
  
using R = long double; // Rにmint渡せるようにする  
using P = complex<R>;  
struct C {  
    P c; R r;  
    C() {}  
    C(const P &a, const R &b) : c(a), r(b) {}  
};  
  
const R EPS = 1e-8;  
const R PI = atanl(1)*4;  
  
inline int sgn(const R& r) { return (r>EPS) - (r<-EPS); }  
inline R dot(const P& a, const P& b) {  
    return real(a)*real(b) + imag(a)*imag(b);  
}  
inline R det(const P& a, const P& b) {  
    return real(a)*imag(b) - imag(a)*real(b);  
}  
namespace std {  
    bool operator < (const P& a, const P& b) {  
        return sgn(real(a-b)) ? real(a-b) < 0 : sgn(imag(a-b)) < 0;  
    }  
    bool operator == (const P& a, const P& b) {  
        return sgn(real(a-b)) == 0 && sgn(imag(a-b)) == 0;  
    }  
    bool cmp_y (const P& a, const P& b) {  
        return sgn(imag(a-b)) ? imag(a-b) < 0 : sgn(real(a-b)) < 0;  
    }  
}  
  
// 線分abから見たcの位置  
enum CCW{LEFT=1, RIGHT=2, BACK=4, FRONT=8, ON_SEG=16};  
int ccw(P a, P b, P c) {  
    P p = (c-a)/(b-a);  
    if(sgn(imag(p)) > 0) return LEFT;  
    if(sgn(imag(p)) < 0) return RIGHT;  
    if(sgn(real(p)) < 0) return BACK;  
    if(sgn(real(p)-1) > 0) return FRONT;  
    return ON_SEG;  
}  
  
// 交差  
int intersect(const C& a, const C& b) {  
    R dist = norm(a.c-b.c), r1 = (a.r+b.r)*(a.r+b.r), r2 = (a.r-b.r)*(a.r-b.r);  
    if(sgn(r1-dist) < 0)  return 4;    // 円が離れている  
    if(sgn(r1-dist) == 0) return 3;   // 外接  
    if(sgn(r2-dist) < 0 && sgn(dist-r1) < 0) return 2; // 交差  
    if(sgn(dist-r2) == 0) return 1; // 内接  
    return 0;    // 内部に含む  
}  
  
// 交点 交差の確認を先にすること！！！  
// intersect=2 を確認すること  
vector<P> crosspoint(C a, C b) {  
    R d = abs(a.c-b.c);  
    R t = (a.r*a.r-b.r*b.r+d*d)/2/d, h = sqrt(a.r*a.r-t*t);  
    P m = t/abs(b.c-a.c)*(b.c-a.c)+a.c;  
    P n(-(a.c-b.c).imag()/abs(a.c-b.c), (a.c-b.c).real()/abs(a.c-b.c));  
    vector<P> ret(2, m);  
    ret[0] -= h*n; ret[1] += h*n;  
    return ret;  
}  
  
// 2円の共通面積を求める  
R common_area(C c1, C c2) {  
    ll type = intersect(c1, c2);  
    if(type >= 3) return 0;  
    if(type <= 1) {  
        ll r = min(c1.r, c2.r);  
        return PI*r*r;  
    }  
    if(c1.r > c2.r) swap(c1, c2);  
    vector<P> ps = crosspoint(c1, c2);  
    R ang1 = acosl(dot(ps[0]-c1.c, ps[1]-c1.c) / (c1.r * c1.r));  
    R ang2 = acosl(dot(ps[0]-c2.c, ps[1]-c2.c) / (c2.r * c2.r));  
    if(ccw(ps[0], ps[1], c1.c) == ccw(ps[0], ps[1], c2.c)) ang1 = max(ang1, 2*PI - ang1);  
    else ang1 = min(ang1, 2*PI - ang1);  
    ang2 = min(ang2, 2*PI-ang2);  
    return c1.r*c1.r*0.5*(ang1-sinl(ang1)) + c2.r*c2.r*0.5*(ang2-sinl(ang2));  
}  
  
int main(void) {  
    ll x1, y1, r1, x2, y2, r2;  
    cin >> x1 >> y1 >> r1 >> x2 >> y2 >> r2;  
    C c1({{x1, y1}, r1}), c2({{x2, y2}, r2});  
  
    cout << fixed << setprecision(9) << common_area(c1, c2) << endl;  
  
    return 0;  
}

Educational Codeforces Round 83 E - Array Shrinking

codeforces

問題ページ

幅が小さい区間から順に参照していくようなDPである、区間DPをします。

区間 \lbrack l,m \rbrack , \lbrack m+1,r \rbrack をマージするときに操作を行って長さを減少させるのは、 \lbrack l,m \rbrack , \lbrack m+1,r \rbrack が両方とも長さ1で、値が同じときだけ考えればよいです。これ以外のときに A_m = A_{m+1} に操作を行うようなことを考慮しなくても大丈夫です。なぜなら、DPの遷移的にすでに A_m = A_{m+1} に操作を行うような列について考えているからです。

#include <bits/stdc++.h>  
using namespace std;  
using ll = long long;  
using PII = pair<ll, ll>;  
#define FOR(i, a, n) for (ll i = (ll)a; i < (ll)n; ++i)  
#define REP(i, n) FOR(i, 0, n)  
#define ALL(x) x.begin(), x.end()  
template<typename T> void chmin(T &a, const T &b) { a = min(a, b); }  
template<typename T> void chmax(T &a, const T &b) { a = max(a, b); }  
struct FastIO {FastIO() { cin.tie(0); ios::sync_with_stdio(0); }}fastiofastio;  
#ifdef DEBUG_   
#include "../program_contest_library/memo/dump.hpp"  
#else  
#define dump(...)  
#endif  
const ll INF = 1LL<<60;  
  
int main(void) {  
    ll n;  
    cin >> n;  
    vector<ll> a(n);  
    REP(i, n) cin >> a[i];  
  
    vector<vector<ll>> dp(n, vector<ll>(n, INF));  
    vector<vector<ll>> val(n, vector<ll>(n, -1));  
    REP(i, n) dp[i][i] = 1, val[i][i] = a[i];  
    FOR(w, 2, n+1) REP(l, n-w+1) {  
        ll r = l+w-1;  
        FOR(i, l, r) {  
            if(dp[l][i] == 1 && dp[i+1][r] == 1 && val[l][i] == val[i+1][r]) {  
                chmin(dp[l][r], 1LL);  
                val[l][r] = val[l][i] + 1;  
            } else {  
                chmin(dp[l][r], dp[l][i] + dp[i+1][r]);  
            }  
        }  
    }  
    cout << dp[0][n-1] << endl;  
  
    return 0;  
}

Educational Codeforces Round 83 D - Count the Arrays

codeforces

問題ページ

数列内の一番大きい数を x とします。同じ数のペアを y (y \lt x) とします。このときの数列は \cdots\ y\ \cdots\ x\ \cdots\ y\ \cdots となっています。y の選び方は x-1 通りあります。

数列に存在する数として x-2 個から n-3 個を選びます。これは \binom{x-2}{n-3} 通りあります。

n-3 個の数を x の左と右のどちらにするか？を決めます。単調増加な列にするので、数の集合さえ決めれば列は一意に定まります。これは 2^{n-3} 通りあります。

各 x について存在する数列が何通りあるか数え、足し上げることで答えが求まります。つまり、答えは \sum_{x=n-1}^{m} (x-1) \times 2^{n-3} \binom{x-2}{n-3} です。

#include <bits/stdc++.h>  
using namespace std;  
using ll = long long;  
using PII = pair<ll, ll>;  
#define FOR(i, a, n) for (ll i = (ll)a; i < (ll)n; ++i)  
#define REP(i, n) FOR(i, 0, n)  
#define ALL(x) x.begin(), x.end()  
template<typename T> void chmin(T &a, const T &b) { a = min(a, b); }  
template<typename T> void chmax(T &a, const T &b) { a = max(a, b); }  
struct FastIO {FastIO() { cin.tie(0); ios::sync_with_stdio(0); }}fastiofastio;  
#ifdef DEBUG_   
#include "../program_contest_library/memo/dump.hpp"  
#else  
#define dump(...)  
#endif  
const ll INF = 1LL<<60;  
  
template<ll MOD>  
struct modint {  
    ll x;  
    modint(): x(0) {}  
    modint(ll y) : x(y>=0 ? y%MOD : y%MOD+MOD) {}  
    static constexpr ll mod() { return MOD; }  
    // e乗  
    modint pow(ll e) {  
        ll a = 1, p = x;  
        while(e > 0) {  
            if(e%2 == 0) {p = (p*p) % MOD; e /= 2;}  
            else {a = (a*p) % MOD; e--;}  
        }  
        return modint(a);  
    }  
    modint inv() const {  
        ll a=x, b=MOD, u=1, y=1, v=0, z=0;  
        while(a) {  
            ll q = b/a;  
            swap(z -= q*u, u);  
            swap(y -= q*v, v);  
            swap(b -= q*a, a);  
        }  
        return z;  
    }  
    // Comparators  
    bool operator <(modint b) { return x < b.x; }  
    bool operator >(modint b) { return x > b.x; }  
    bool operator<=(modint b) { return x <= b.x; }  
    bool operator>=(modint b) { return x >= b.x; }  
    bool operator!=(modint b) { return x != b.x; }  
    bool operator==(modint b) { return x == b.x; }  
    // Basic Operations  
    modint operator+(modint r) const { return modint(*this) += r; }  
    modint operator-(modint r) const { return modint(*this) -= r; }  
    modint operator*(modint r) const { return modint(*this) *= r; }  
    modint operator/(modint r) const { return modint(*this) /= r; }  
    modint &operator+=(modint r) {  
        if((x += r.x) >= MOD) x -= MOD;  
        return *this;  
    }  
    modint &operator-=(modint r) {  
        if((x -= r.x) < 0) x += MOD;  
        return *this;  
    }  
    modint &operator*=(modint r) {  
    #if !defined(_WIN32) || defined(_WIN64)  
        x = x * r.x % MOD; return *this;  
    #endif  
        unsigned long long y = x * r.x;  
        unsigned xh = (unsigned) (y >> 32), xl = (unsigned) y, d, m;  
        asm(  
            "divl %4; \n\t"  
            : "=a" (d), "=d" (m)  
            : "d" (xh), "a" (xl), "r" (MOD)  
        );  
        x = m;  
        return *this;  
    }  
    modint &operator/=(modint r) { return *this *= r.inv(); }  
    // increment, decrement  
    modint operator++() { x++; return *this; }  
    modint operator++(signed) { modint t = *this; x++; return t; }  
    modint operator--() { x--; return *this; }  
    modint operator--(signed) { modint t = *this; x--; return t; }  
    // 平方剰余のうち一つを返す なければ-1  
    friend modint sqrt(modint a) {  
        if(a == 0) return 0;  
        ll q = MOD-1, s = 0;  
        while((q&1)==0) q>>=1, s++;  
        modint z=2;  
        while(1) {  
            if(z.pow((MOD-1)/2) == MOD-1) break;  
            z++;  
        }  
        modint c = z.pow(q), r = a.pow((q+1)/2), t = a.pow(q);  
        ll m = s;  
        while(t.x>1) {  
            modint tp=t;  
            ll k=-1;  
            FOR(i, 1, m) {  
                tp *= tp;  
                if(tp == 1) { k=i; break; }  
            }  
            if(k==-1) return -1;  
            modint cp=c;  
            REP(i, m-k-1) cp *= cp;  
            c = cp*cp, t = c*t, r = cp*r, m = k;  
        }  
        return r.x;  
    }  
  
    template<class T>  
    friend modint operator*(T l, modint r) { return modint(l) *= r; }  
    template<class T>  
    friend modint operator+(T l, modint r) { return modint(l) += r; }  
    template<class T>  
    friend modint operator-(T l, modint r) { return modint(l) -= r; }  
    template<class T>  
    friend modint operator/(T l, modint r) { return modint(l) /= r; }  
    template<class T>  
    friend bool operator==(T l, modint r) { return modint(l) == r; }  
    template<class T>  
    friend bool operator!=(T l, modint r) { return modint(l) != r; }  
    // Input/Output  
    friend ostream &operator<<(ostream& os, modint a) { return os << a.x; }  
    friend istream &operator>>(istream& is, modint &a) {   
        is >> a.x;  
        a.x = ((a.x%MOD)+MOD)%MOD;  
        return is;  
    }  
    friend string to_frac(modint v) {  
        static map<ll, PII> mp;  
        if(mp.empty()) {  
            mp[0] = mp[MOD] = {0, 1};  
            FOR(i, 2, 1001) FOR(j, 1, i) if(__gcd(i, j) == 1) {  
                mp[(modint(i) / j).x] = {i, j};  
            }  
        }  
        auto itr = mp.lower_bound(v.x);  
        if(itr != mp.begin() && v.x - prev(itr)->first < itr->first - v.x) --itr;  
        string ret = to_string(itr->second.first + itr->second.second * ((int)v.x - itr->first));  
        if(itr->second.second > 1) {  
            ret += '/';  
            ret += to_string(itr->second.second);  
        }  
        return ret;  
    }  
};  
using mint = modint<998244353>;  
  
// 前計算O(N) クエリO(1)  
mint combi(ll N, ll K) {  
    const int maxN=5e5; // !!!  
    static mint fact[maxN+1]={},factr[maxN+1]={};  
    if (fact[0]==0) {  
        fact[0] = factr[0] = 1;  
        FOR(i, 1, maxN+1) fact[i] = fact[i-1] * i;  
        factr[maxN] = fact[maxN].inv();  
        for(ll i=maxN-1; i>=0; --i) factr[i] = factr[i+1] * (i+1);  
    }  
    if(K<0 || K>N) return 0; // !!!  
    return factr[K]*fact[N]*factr[N-K];  
}  
  
int main(void) {  
    ll n, m;  
    cin >> n >> m;  
  
    mint ret = 0;  
    FOR(i, n-1, m+1) ret += (i-1) * combi(i-2, n-3);  
    ret *= mint(2).pow(n-3);  
  
    cout << ret << endl;  
  
    return 0;  
}

dp[i番目まで][最後がj] から考察をはじめた結果、一生高速にならなくて終了した
最大の数だけ決めればよくて、i番目はあんまり気にしなくていい