ネットワークフロー - ferinの競プロ帳

最近フロー関連をやってたのでそのメモ

最大流

$N$ 頂点 $M$ 辺の有向グラフ各辺 $e$ には容量 $c(e)$ が定義されている
$\delta_{+}(v), \delta_{-}(v)$ をそれぞれ頂点 $v$ から出る/入る辺の集合とする
始点を $s$ ，終点を $v$ とする

LPの形で書くと以下の通り
$\text{maximize } \sum_{e\in\delta_{+}(v)} f(e)$
$\text{s.t. } 0 \leq f(e) \leq c(e)$
$\sum_{e\in\delta_{-}(v)} f(e) = \sum_{e\in\delta_{-}(v)} f(e)\ \ \ \ (v\in V\setminus{s,t})$

ford-fulkerson

最大流を求めるアルゴリズムの一つ最大流の流量を $F$ として $O(FE)$

用語定義

残余グラフ: $f(e)\lt c(e)$ である辺 $e$ および， $f(e)\gt 0$ である辺 $e$ の逆辺から成るグラフ
増加パス: 残余グラフ上のs-tパス

増加パスが存在したらそのパスに沿って目一杯フローを流す．この処理を増加パスが存在しなくなるまで繰り返す．

最大フロー最小カット定理

最大のs-tフロー = 最小のs-tカット

ford-fulkerson，最大フロー最小カット定理の証明は蟻本p191
ford-fulkersonで最大流が求まることから，存在性・容量が整数であればフローも整数であることがわかる

増加パスが存在しない $\iff$ 残余グラフに対応するフローが最大流からも証明できる
最大フロー最小カット定理はLPの双対定理からも確認できる　

LPとグラフと定式化 by とこはるさんの2.2節
ネットワークフロー入門 by hosさんのⅢ

最小カットの復元
最大フローに対応する残余グラフにはs-tパスが存在しない．残余グラフで始点 $S$ から到達できる頂点の集合を $X$ ，到達できない頂点の集合を $Y$ とするとカット $(X,Y)$ は最小カットである．

Dinic

最大流を求めるアルゴリズムの一つ最悪 $O(EV^2)$ だが多くのケースで高速に動作する
参考資料

最大流問題について. by Mi_Sawaさん
蟻本p194

Dinic法の正当性は増加パスが存在しない $\iff$ 残余グラフに対応するフローが最大流から証明できる
特殊なグラフなら高速に動作する保証つき

二部マッチング → $O(E\sqrt{V})$
Hopcroft-karpはDinicで最大流を流すのと同じ(だったはず)
二部マッチングでTLEに苦しんだ話 by snukeさん高速な二部マッチング
$6e5$ 頂点 $4e5$ 辺の二部グラフの最大マッチングが225ms 提出
辺の重みが同じ → $O(\min(E^{1/2}, V^{2/3}))$

自分の実装

さまざまなグラフについての最大流 (蟻本p192)

複数の始点・終点が存在する場合

super-source・super-sink をつくればよい．これは最大流に限った話ではなく最短経路などのグラフの問題一般でよくでてくる．多品種フロー（効率的にはとけない）との混合に注意．
多品種フロー: 始点 $s_i$ からは終点 $t_j$ に行くなど，始点と終点に対応関係が存在するもの

例題(フローではないけどこのテクを使う)

無向グラフ

両方向に有向辺を貼ったグラフで考えればいい

頂点容量

頂点 $v$ を入頂点と出頂点に分割し， $v$ に入る辺は入頂点， $v$ から出る頂点は出頂点へと接続する．入頂点から出頂点への辺の容量を頂点の容量とすることで辺容量に置き換えられる．

最小流量制約

辺 $e$ に最小流量 $b(e)$ の制約が存在する場合の最大フローの求め方
頂点 $S,T$ を新たに作成する．辺 $e=(u,v)$ が存在する場合， $S$ から $v$ に容量 $b(e)$ ， $u$ から $v$ に容量 $c(e)-b(e)$ ， $u$ から $T$ に容量 $c(e)$ の有向辺を貼る． $S$ から $s$ へ $\infty$ ， $t$ から $T$ へ $\infty$ の有向辺を貼る． $S$ から $T$ への最大流を $F'$ とすると元のグラフの最大流は $F=F'-\sum_{e\in E} b(e)$

f:id:ferin_tech:20191028183404j:plain

$u$ から $T$ にフローが流れていれば $u$ へ流量1が入ることが確定するため最小流量制約はクリアしている．
$S$ から $v$ へフローを流すことで $v$ に流量1が確定して流れるようなグラフを構成している．

存在しない場合のcheck
$S$ から $s$ ， $t$ から $T$ への有向辺をはらずずに $t$ から $s$ へ容量 $\infty$ の辺を貼る． $S$ から $T$ へ流量 $\sum_{e\in E} b(e)$ が流れるか？

f:id:ferin_tech:20191028183802j:plain

これがクリアできる $\iff u$ から $T$ の辺のフローが全て流れている
クリアできないグラフは上の画像のように弾かれる

最小流量制限付き最大流 by snukeさん
$S$ から $s$ ， $t$ から $T$ の辺を貼らずに $S \to T, s \to T, S \to t, s \to t$ の最大流を順番に流す方法が簡単．

グラフを変形

容量を増やす場合 → そのまま流せばいい
辺 $e$ の容量を1減らす → $f(e)-1 \leq c(e)$ ならそのまま，それ以外なら残余グラフで押し戻す
詳しくは問題例のBox Witchのあたりに書いた

容量が負

NP-hardなので難しいが変形で消せる場合もある

最小費用流

始点から終点に水を流す問題に見えがちだが，定義上始点と終点は不必要
最小費用流の負辺除去 by snukeさん

LPで定義する
双対性 by wataさんのp43に詳しい
変数定義
有向グラフ $G=(V,E)$
各辺 $e\in E$ に対して

容量 $c(e) \geq 0$
コスト $d(e) \in \mathbb{R}$

需要供給関数 $b:V\to\mathbb{R}$
$\delta_{+}(v), \delta_{-}(v) \to$ それぞれ頂点 $v$ から出る/入る辺の集合

イメージ
$b(v)\gt0$ の頂点では水が $b(v)$ 湧き出る
$b(v)=0$ の頂点では水が入る量=出る量 $b(v)\lt0$ の頂点では水が $b(v)$ 不足
辺 $e$ は $c(e)$ まで流せ，流量1ごとにコスト $d(e)$ がかかる

定式化
$\text{minimize } \sum_{e\in\delta_{+}(v)} f(e)$
$\text{subject to }\ 0 \leq f(e) \leq c(e)\ \ \ \ (\forall e \in E)$
$\sum_{e\in\delta_{-}(v)} f(e) - \sum_{e\in\delta_{-}(v)} f(e) = -b(v)\ \ \ \ (v\in V)$

実装については最小費用流の負辺除去 by snukeさんに載っている

蟻本形式の実装の場合
* $b(v)$ が正: $S$ から $v$ へ容量 $b(v)$ コスト0の辺
* $b(v)$ が負: $v$ から $T$ へ容量 $-b(v)$ コスト0の辺

とすればよい

始点 $s$ から終点 $t$ へ流量 $F$ を流す → $b(s)=F, b(t)=-F$ と帰着できる(はず)でよく見るのと同義

最短路反復法

最小費用流を求めるアルゴリズムの一つ

参考資料

ネットワークフロー入門 by hosさんのp56
蟻本p200

辺容量 $c(e)$ と流量 $F$ は整数，入力に負閉路は存在しないとする
残余グラフ: $f(e)\lt c(e)$ である辺はコスト $d(e)$ ， $f(e)\gt 0$ である辺の逆辺はコスト $-d(e)$

流量が $F$ 以下の間以下を繰り返す

残余グラフでまだ流せる辺のみを使ってコストを重みとした最短路問題を解く
最短路が存在しなければ流量 $F$ のフローが存在しない
最短路に沿ってフローを目一杯流す

負辺があるため最短路をBellman-Fordで求めると $O(F|V||E|)$

証明の方針) 残余グラフに負閉路が存在しない $\iff$ 残余グラフに対応するフローが最小費用流
アルゴリズム終了時に負閉路は存在しない

ポテンシャルを考えると負辺が存在するグラフもdijkstraで解ける → $O(F|E|log|V|)$
入力に負辺がある場合，一回目だけBellman-Fordをすればよい → $O(F|E|log|V| + |E||V|)$
負閉路が存在しているならばBellman-Fordで検出し，そこに目一杯流すと負閉路を消せるこれよくわかってない

これは流量 $F$ に比例する計算量なので擬多項式時間アルゴリズム
 最小費用最大流の悪例題 by Min_25さんに指数時間かかる例がある

自分の実装

---ToDo---
別のアルゴリズム

容量スケーリング
最小平均長閉路解消
コストスケーリング

---ToDo---

さまざまなグラフについての最小費用流 (蟻本p204)

複数の始点・終点が存在する場合

最大流と同じ super-source・super-sinkを使えばいい

頂点容量

最大流と同じ頂点を2倍にして辺容量にする

無向グラフ

頂点2倍

最小流量制約

$e=(u,v)$ に最小流量 $b(e)$ が存在する場合辺 $e'$ を追加する
$c'(e)=c(e)-b(e), d'(e)=d(e), c'(e')=b(e), d'(e')=d(e)-M$ $M$ は十分大きな定数
このグラフでの最小費用流 $+ M \times \sum_e b(e)$ が答えになる

$e'$ のコストの方が非常に小さいので $b(e)$ の分は必ず流れる
$b(e)$ 流せない辺があったら答えが $M$ 以上にになるからわかる(はず)

流す流量が任意

負辺を含むグラフでできるだけ小さくしてくださいみたいな問題
最短経路にフローを流して，最短路が短くなることはない $\iff h_{i+1}(v) \geq h_i(v)$
$h_i(t) = (s$ から $t$ までの最短距離 $)$ が負の間流し続ければよい

負辺の除去

最小費用流の負辺除去 by snukeさん

応用例

マッチング・辺カバー・安定集合・点カバー

二部グラフの最小点被覆、最大安定集合 (最大独立集合)、最小辺被覆を総整理！ by drkenさん
 GabowのEdmonds' Algorithm(一般マッチング O(VElogV))の解説と実装

一般マッチングは多項式時間で求まる（がめっちゃ複雑）
マッチングの大きさのみで復元がいらないならばTutte行列を使って $O(N^3)$ で求まる提出

project selection problem・燃やす埋める問題

ferin-tech.hatenablog.com

問題例

主に競技プログラミングにおける最大流問題まとめ by hamayanhamayanさんを解いています

最大流

verify用の問題

ARC074 F - Lotus Leaves

最小カットそのまま

No.177 制作進行の宮森あおいです！

最大フローに帰着する https://yukicoder.me/submissions/390377

No.654 Air E869120

各街について時刻の分頂点をつくれば最大フローで解けるがこれは無理
各町に関連する時刻は飛行機が出発/到着する時刻のみなので座圧すれば問題ない
https://yukicoder.me/submissions/390383

CodeChef Bipartite Graph from Trees

概要

$N$ 頂点の木， $M$ 個の頂点集合 $A_i$ が与えられる
二部グラフ $G=({l_1,\ldots,l_M},{r_1,\ldots,r_N},E)$ を考える
$j$ の祖先が頂点集合 $A_i$ に含まれる場合 $l_i$ と $r_j$ をつなぐ辺を追加する
$G$ の最大マッチングを求めろ

$N,M \leq 5000$

解説

二部グラフ $G$ の辺を定義通りに追加すると $5000^2$ 程度になり間に合わない
$A_i$ の要素である頂点の子孫全てに辺を貼る部分をどうにかして辺を減らしたい
木の親から子に容量 $\infty$ の辺を貼って置くことで子孫に貼る必要はなくなる
頂点数 $N+M+2$ で辺数 $O(N+M)$ まで削減できたのでdinic等で最大フローを求められる

Codeforces Round #304 (Div. 2) E. Soldier and Traveling

概要

$n$ 頂点 $m$ 辺の無向グラフが与えられる
頂点 $i$ には最初 $a_i$ 人が存在し，各人は高々一つまでの辺を使って移動ができる(留まることもできる)
移動後に頂点 $i$ に $b_i$ 人が存在するような移動は存在するか？
存在する場合移動の方法の復元も含めて出力しろ

$n \leq 100, m \leq 200$

解説

$L=$ 移動前を表す $n$ 頂点， $R=$ 移動後を表す $n$ 頂点，始点，終点の計 $2n+2$ 頂点を用意する．

始点から $L$ の $i$ 番目の頂点へ容量 $a_i$ の辺
$R$ の $i$ 番目の頂点から終点へ容量 $b_i$ の辺
入力のグラフで $i$ から $j$ へ移動可能ならば， $L$ の $i$ 番目の頂点から $R$ の $j$ 番目の頂点へ容量 $\infty$ の辺

$\sum a_i = \sum b_i$ かつ始点から終点への最大流が $\sum b_i$ と一致するならばYES
$L$ の $i$ 番目の頂点から $R$ の $j$ 番目の頂点へ流量 $f$ のフローが流れているならば $i$ から $j$ へ $f$ 人が移動した(留まった)と言える

Waiwai Otaku Panic

最短経路のみを考えるので入力のグラフを最短路DAGに変形する
最短路DAG: ある終点への最短路に使われうる辺のみを抽出したグラフ DAGになる

頂点0からの最短経路長が一致しない頂点からスタートする車はある辺を同じタイミングで移動することはない
したがって最短経路長ごとに頂点を分割して考える
集合 $S_i$ を最短経路長が $i$ の頂点の集合とする

super-sourceから $S_i$ の頂点 $j$ へ容量 $a_j$ の辺を貼る
最短路DAGの辺を容量 $1$ とする(同時に通らないように)
このグラフの最大流を求め， $\sum_{j \in S_i} a_j$ と一致するならばok
全ての $S_i$ に対してこの操作を行う https://www.hackerrank.com/contests/camypapercon02/challenges/waiwai-otaku-panic/submissions/code/1317045120

Infinite Network

$|x|,|y| \leq 100$ より $x=101$ もしくは $x=-101$ もしくは $y=101$ もしくは $y=-101$ の点集合 $(=P$ とする $)$ にウイルスが来なければ有限個に抑えられる

始点から感染したコンピューターへ容量 $\infty$
$P$ から終点へ容量 $\infty$
隣り合ったコンピュータ同士で容量 $1$

このグラフで最小カット(=最大フロー)を求めればよい https://www.hackerrank.com/contests/unkoder-06/challenges/infinite-network/submissions/code/1317047943

KUPC2016 E - 柵 / Fences

Infinite Networkと大体同じ
切断する部分がマスで頂点なので頂点条件から辺条件に置き換える必要がある
頂点制約と同様に各マスに2つ頂点を用意し，それぞれマスに入る/出る頂点とすればよい

https://atcoder.jp/contests/kupc2016/submissions/8008433

TTPC2015 L - グラフ色ぬり

青い辺を追加しても最大流が増えない $\iff$ 追加した辺集合の任意の辺があるカットに含まれない
カットとして青い辺が含まれる数が最小になるカットを求め，それ以外の青い辺を追加すると考えればよい
カットに含まれる青い辺を減らすには赤い辺の容量を増やして，最小カット(=最大フロー)を求めればよい

https://atcoder.jp/contests/ttpc2015/submissions/8011585

ARC031 D - 買い物上手

変数

$S_i$ : $i$ 番目の組合せでもらえる経験値 (入力)
$T_i$ : $i$ 番目のアイテムの値段 (入力)

平均の最大化は二分探索が典型
$x=$ 得た経験値 $/$ 使った金とする．得た経験値 $-x \times$ 使った金 $=0$ である $x$ を求めればよい．よって得た経験値 $-x \times$ 使った金を最大化できればよい．この問題をIPで定式化する．

変数

$x$ : 得た経験値 $/$ 使った金 (given)
$\text{exp}'_{i}$ : $i$ 番目の組合せを取得するか？の01変数
$\text{item}'_{i}$ : $i$ 番目のアイテムを買うか？の01変数

$\text{maximize } \sum_{i=1}^N S_i\text{exp}'_{i} - x\sum_{i=1}^M T_i\text{item}'_{i}$
$\text{s.t. } \text{exp}'_i=1 \Rightarrow \text{item}'_j=1$ ( $i$ 番目の組合せにアイテム $j$ が含まれる)

$\text{exp}'_i=1 \Rightarrow \text{item}'_i=1$ は不等式ではないが $\text{exp}'_i \leq \text{item}'_j$ と等価なのでIPと言える．一般に $\Rightarrow$ (ならば) を数理計画で扱いたいときはbig-M法などを用いることで不等式に変換することができることがある．
$S_i\gt0, T_i\gt0$ より $\text{exp}'_{i}, \text{item}'_{i}$ は連続変数(実数値を取る変数)としても答えが悪化しない．したがってIPからLPに変形することができた．01変数や整数変数などを連続変数にすることを連続緩和と呼ぶ．

変数

$\text{exp}_{i}$ : $\text{exp}'_{i}$ の連続緩和
$\text{item}_{i}$ : $\text{item}'_{i}$ の連続緩和

$\text{maximize } \sum_{i=1}^N S_i\text{exp}_{i} - x\sum_{i=1}^M T_i\text{item}_{i}$
$\text{s.t. } \text{exp}_i \leq \text{item}_j$ ( $i$ 番目の組合せにアイテム $j$ が含まれる)
$\text{exp}_i \leq 1$
$\text{item}_i \geq 0$

このLPの双対問題を考える．
-----わからん-----
双対性 by wataさんのp14~に沿って変形をする． $\text{exp}_i - \text{item}_j \leq 0$ の両辺に $x_{ij}$ ， $\text{exp}_i \leq 1$ の両辺に $y_i$ を掛けて足し合わせる． $\sum_{j=1}^M x_{1j}\text{exp}_1 + \cdots + \sum_{j=1}^M x_{Nj}\text{exp}_N - \sum_{i=1}^N x_{i1}\text{item}_1 - \cdots - \sum_{i=1}^N x_{iM}\text{item}_M \leq \sum_{i=1}^N y_i$ となる．元問題の目的関数の係数と比較すると $\sum_{j=1}^M x_{ij}+y_i \geq S_i, -\sum_{i=1}^N x_{ij} \geq -xT_j$ となる．

$\text{minimize } \sum_{i} y_i$
$\text{s.t. } \sum_{j} x_{ij} + y_i \leq S_i\ \ \ (1 \leq i \leq N)$
$\sum_{i} x_{ij} \leq xT_j\ \ \ (1 \leq j \leq M)$
$x_{ij} \geq 0$ ( $i$ 番目の組合せにアイテム $j$ が含まれる)
$y_i \geq 0$

どうやってもこのpdfの変形と一致しないけど最初の制約式 $\leq$ じゃなくて=なのなんで？ $y_i$ の消し方もよくわからん http://www.orsj.or.jp/~archive/pdf/bul/Vol.42_06_440.pdf
-----わからん-----

$\text{maximize } \sum_{ij} x_{ij} - \sum_{i} S_i$
$\text{s.t. } \sum_{j} x_{ij} \leq S_i\ \ \ (1 \leq i \leq N)$
$\sum_{i} x_{ij} \leq xT_j\ \ \ (1 \leq j \leq M)$
$x_{ij} \geq 0$ ( $i$ 番目の組合せにアイテム $j$ が含まれる)

これは二部グラフの最大流と同義

経験値を得られる組合せに対応する $N$ 個の頂点，アイテムに対応する $M$ 個の頂点，始点，終点の $N+M+2$ 個の頂点からなるグラフを考える．

始点から組合せ $i$ に容量 $S_i$
アイテム $j$ から終点に容量 $xT_j$
組合せ $i$ からアイテム $j$ に容量 $\infty$ (アイテム $j$ が組合せ $i$ に含まれる)

この最大流 $(=\sum_{i} x_{ij})$ が

$\sum_{i} S_i$ 以上なら $x$ が小さい
$\sum_{i} S_i$ 未満なら $x$ が大きい

として二分探索

https://atcoder.jp/contests/arc031/submissions/8015301

Educational Codeforces Round 8 F. Bear and Fair Set

概要

Limakは $n$ 要素( $n$ は5の倍数)の集合を持っている
この集合の要素は1以上 $b$ 以下である
要素を $\text{mod}\ 5$ した値が0,1,2,3,4のものがそれぞれ $5/n$ 個含まれる

1以上 $a$ 以下の要素が $x$ 個含まれるというヒントが $q$ 個与えられる
ヒントに矛盾しない集合が存在するかどうか？の判定を行え

$n \leq b \leq 10^4, q \leq 10^4$

解説

ヒントについて $a$ でソートすることで，区間 $\lbrack 1,a_1 \rbrack, \lbrack a_1+1, a_2 \rbrack, \ldots, \lbrack a_q, b \rbrack$ に何個要素が存在するか？と変形できる
この時点で矛盾が存在する場合"unfair"を出力して終了する

区間と余り0~4で対応をつける
区間 $q+1$ 個，余り0～4の5個，始点，終点の計 $q+7$ 頂点から成るグラフを考える

始点から区間 $i$ に容量がその区間に含まれる要素数である辺
余り $i$ から終点へ容量 $n/5$ の辺
区間 $i$ から余り $j$ に容量がその区間に含まれる余り $j$ の個数である辺

このグラフで最大流が $n$ ならば"fair"，それ以外なら"unfair"を出力する

RUPC2018 day3 F：最短距離を伸ばすえびちゃん

最短経路について考えるので最短路DAGに変形する
最短距離を伸ばす場合，最短路DAGのカットの辺を1ずつ伸ばせば最短距離が1伸びる
したがって容量を $c_i$ とした有向辺を貼り，最小カットを求めればよい

https://onlinejudge.u-aizu.ac.jp/beta/review.html#RitsCamp18Day3/3939898

AOJ2168 Luigi's Tavern

マッチングをグラフで表して最大流を求める
http://judge.u-aizu.ac.jp/onlinejudge/review.jsp?rid=3940110#1

AOJ2168 Luigi's Tavern by nanikakaさん

AOJ2835 敵襲から守れ

f:id:ferin_tech:20191028185054j:plain
f:id:ferin_tech:20191028185128j:plain

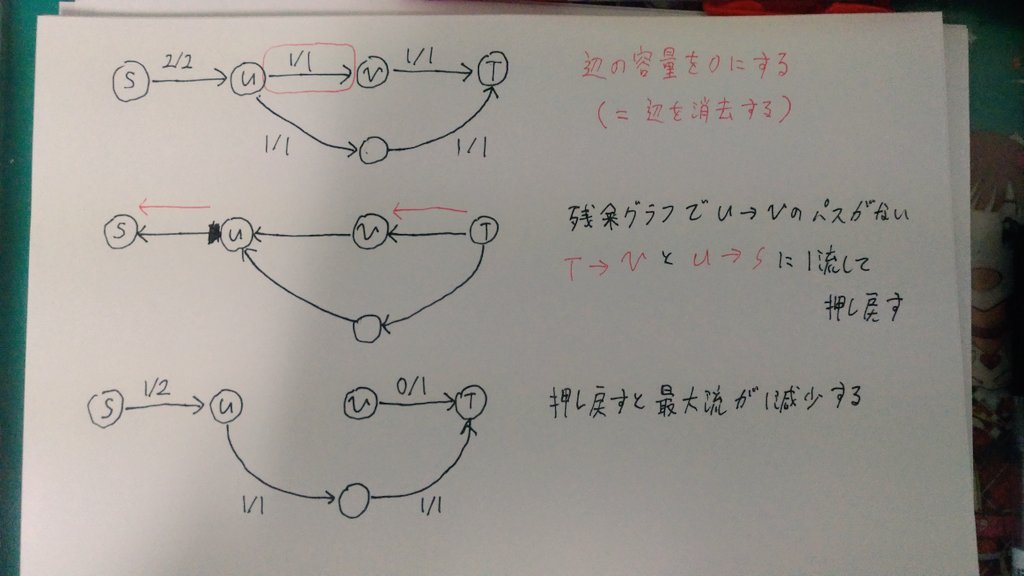
辺容量が1の辺を無視したグラフで最小カットを求めればよい．しかし，愚直にやると最大流の計算を $O(E)$ 回やることになって間に合わない．そこで，蟻本p193のグラフを変形する場合に書かれているテクニックを使う．
まず入力のグラフについて最大流を求めておく．次に容量が1の辺 $e$ の容量を0にした後，最大流を計算する．この最大流が入力のグラフの最大流よりも小さければ，それが達成できる最小である．
容量を1減らしたときの最大流の再計算は以下の3パターンのいずれかで計算できる

辺 $e=(u,v)$ について $f(e) \leq c(e)-1$
そのまま辺容量を1減らす
$f(e)=c(e)$ かつ ( $u$ から $v$ に残余グラフでパスが存在 $\iff$ $u$ から $v$ へ流量1のフローが流せる)
$u$ から $v$ へ押し戻せばよく，最大流の値は変化しない(画像1枚目)
otherwise
$t$ から $v$ と $u$ から $s$ へ押し戻せばよい．最大流の値は1減少(画像2枚目)

よくあるフローの実装では辺 $e$ にcapとして $c(e)-f(e)$ ，逆辺にcapとして $f(e)$ をもたせる．このとき辺容量を1減らすという操作は以下の2パターンのいずれかとなる．

$\text{e.cap}=0 \iff c(e)=f(e)$
$c(e),f(e)$ がともにマイナス1される．よって逆辺のcapをマイナス1すればよい．
$\text{e.cap}\gt0 \iff c(e)\gt f(e)$
$c(e)$ のみマイナス1される．よって辺 $e$ のcapをマイナス1すればよい

http://judge.u-aizu.ac.jp/onlinejudge/review.jsp?rid=3941579#1

AOJ2313 Box Witch

敵襲から守れと同様にグラフを変形する場合に最大流を高速に計算する方法を用いる．
辺を増やすことは辺容量が0から1にすると言い換えられる．辺容量を増やしたあと，0から最大流を計算するのではなく流量1のフローを流すことで最大流を計算できる．流量1のフローはBFS，DFSを1回行えばよいので $O(V+E)$ で計算可能である．
容量を減らす場合は敵襲を守れと同様に計算すればよい．

http://judge.u-aizu.ac.jp/onlinejudge/review.jsp?rid=3941573#1

辺容量を変化させたときに最大流を再計算する方法

辺容量をプラスする場合
単純に始点から終点へフローを流せばよい
流量 $F$ ならば $O(\min(FE, EV^2))$ とかになるのかな…？
辺容量をマイナス1する場合
$O(E)$ でできる
辺容量をマイナス $c$ する場合
残余グラフで $u$ から $v$ のパスでできるだけ押し戻しておく
これで押し戻せなかった分を $t$ から $v$ ， $u$ から $s$ に押し戻す
とかでできる？(ちゃんと確かめてはない)

変化量が $\pm 1$ より大きい場合を問題として面白くするの難しそう
蟻本p193の「最大流のフローが辞書順最小」を最大流に含まれる辺番号の集合が辞書順最小の意味だと思うと，辺番号が最も大きいものの容量を1減らして最大流が減少しなければ，改善されているみたいなのを繰り替えすってことな気がする

yukicoder No.459 C-VS for yukicoder

パック $i$ と列 $x$ のマッチングに帰着すると最小流量制限つき最大流で求められる．

https://yukicoder.me/submissions/392121

最大流について

グラフをうまく構築して辺の数を減らす
頂点制約を辺制約に置き換える
最大フロー・最短距離を増やす → 最小カットの辺を増やす
複数の集合のマッチングをグラフでうまいこと表現
グラフを変形した際に最大流を高速に再計算

あたりの問題があった

ここからは競技プログラミングにおける最大マッチング問題まとめ by hamayanhamayanさんを主に解いています

yukicoder No.241 出席番号(1)

流量が1の辺が最大二部マッチングに含まれるので，二部マッチングの復元ができる．

https://yukicoder.me/submissions/392650

yukicoder No.421 しろくろチョコレート

幸福度が増える量から，方法3,2,1と貪欲に行っていけば良い．方法3で取れるペアが何個あるかわかれば，最大の幸福度がわかる．グリッドグラフは二部グラフであるので，ペアの個数は二部マッチングを用いて数えられる．

https://yukicoder.me/submissions/392796

天下一プログラマーコンテスト2015予選A C - 天下一美術館

しろくろチョコレートとほとんど同じ．隣接している && a[i1][j1]!=b[i1][j1] && a[i2][j2]!=b[i2][j2] && a[i1][j1]!=a[i2][j2] であるような $(i1,j1),(i2,j2)$ のペアが何個あるか数えられればよい．グリッドグラフは二部グラフなので二部マッチングで数えられる．

https://atcoder.jp/contests/tenka1-2015-quala/submissions/8115586

AtCoder Regular Contest 013 D - 切り分けできるかな？

つくることが可能な体積を列挙する．基本的に一つの鉄塊から1つの体積を生成できるため，つくれる体積の種類数 $\times$ 2が答えになる．ただし，一つの鉄塊から使える体積の鉄塊を2つ得た場合，切る必要のある鉄塊が一つ減る．この鉄塊の数を減らせる体積のペアの数を求めたい．
ある鉄塊から体積 $A$ と体積 $B$ の鉄塊が作れるならば， $A$ と $8000+B$ を結んだグラフをつくり二部マッチングを求める．このマッチングが鉄塊を減らせる個数になる．

https://atcoder.jp/contests/arc013/submissions/8116019

CSA Flipping Matrix

概要

$N \times N$ の行列が与えられる．以下の操作を繰り返して，全ての対角成分が1である行列にできるか？できるならば操作の復元も出力せよ．

行を入れ替える
列を入れ替える

解法

左側に行を表す $n$ 頂点，右側に列を表す $n$ 頂点がある二部グラフを考える．行列の $(i,j)$ に1が存在するなら行 $i$ と列 $j$ を結ぶ．この二部グラフで最大マッチングが $n$ でない場合，対角成分が全て1の行列をつくるのは不可能である．
二部マッチングの復元を行い，対応する行と列を求める．この対応にのっとって，列の交換を行っていくことで操作の復元が可能である．

https://csacademy.com/code/4FNXQBaB/

CSA No Prime Sum

概要

$N$ 個の異なる要素からなる集合 $S$ が与えられる．任意の2要素の和が素数でないようにするために取り除く要素数のうち最小のものを求めろ．復元もすること．

解法

$A_i + A_j$ が素数であれば頂点 $i$ と頂点 $j$ を結んだグラフを考える． $A_i + A_j \gt 2$ より素数は奇数しかありえない．したがって偶数と奇数の間にしか辺は存在しないので，これは二部グラフである．
このグラフで辺の端点のうち片方の頂点は少なくとも消去しなければならない．これは最小点カバーで，二部グラフであれば高速に求めることができる．最小点カバーの復元は残余グラフで「到達不可能な左側頂点」「到達可能な右側頂点」とすればよい．
二部グラフの最小点被覆、最大安定集合 (最大独立集合)、最小辺被覆を総整理！ by drkenさん

https://csacademy.com/code/EVEX24Mx/

HackerRank Drawing Rectangles

概要

左下が $(x_1,y_1)$ ，右上が $(x_2,y_2)$ である四角形の領域 $n$ 個に色を塗る．行/列の色を全て消す操作を繰り返し，全ての色を消す．このときの最小の操作回数，およびどのような操作をするか出力せよ．

$n,x_i,y_i \leq 3e5$
色が塗られているマスの数 $\leq 3e5$

解法

左側に行を表す $300000$ 頂点，右側に列を表す $300000$ 頂点を用意した二部グラフを考える．マス $(i,j)$ に色が塗られているならば，行 $i$ と列 $j$ を表す辺をつなぐ．このグラフで最小点カバーを求めることで答えがわかる．
最大でも $V \approx 600000, E \approx 300000$ 程度なので dinicで $O(E\sqrt{V})$ で最大マッチングを求めることができる．

色がついているマスを列挙するパートはセグメント木を持ちながら平面走査を行うことでできる．セグメント木で $x=i$ のときの情報を $\text{seg}\lbrack y \rbrack = ($ 座標 $y$ で色が何重に塗られているか $)$ として持つ． $\text{seg}\lbrack y \rbrack \geq 1$ である $y$ を列挙すればよい．

https://www.hackerrank.com/contests/university-codesprint-4/challenges/drawing-rectangles/submissions/code/1317227391

Maximum-Cup 2018 H - Maxmin Tour

最大値の最小化なので二分探索で判定問題に置き換える． $s_i \leq X$ となるような移動だけでスタンプラリーが可能か？の判定に置き換えることができた．
そもそも $a_i$ から $a_{i+1}$ までの距離が $X$ 以下であれば無条件でこの移動は可能．魔法の石は $a_i$ から $a_{i+1}$ までの間で高々1回しか使用しない．また使用する場合， $a_i$ にいるときに使うべきである．よって，「魔法の石 $b_j$ を使うことで $a_i$ から $a_{i+1}$ への移動が距離 $X$ 以下でできるようになる」と「 $b_j$ から $a_{i+1}$ までの距離が $X$ 以下」は同値である．
地点を表す $k-1$ 個の頂点と魔法の石を表す $Q$ 個の頂点からなる二部グラフを考える．「 $b_j$ から $a_{i+1}$ までの距離が $X$ 以下」であれば，地点 $i$ と魔法の石 $j$ を結ぶ．この二部グラフの最大マッチングが $k-1$ ならば移動が可能と判定できる．

https://atcoder.jp/contests/maximum-cup-2018/submissions/8124730

AOJ2429 まるかいて

初期盤面を全て空白である盤面に帰着する．いったん全ての丸を消去したことにして，その消去コストの和を求めておく．あるマスに丸が存在するようにするには，以下のコストがかかる．

元々空白，書き込みコストの分を足す
元々丸，消去コストの分を引く

行を表す $n$ 個の頂点，列を表す $n$ 個の頂点が存在する二部グラフを考える． $(i,j)$ を丸にするために必要なコストを重みとした辺を行 $i$ と列 $j$ の間に結ぶ．この二部グラフで重み付き最小二部マッチングを求めればよい．
重み付き最小二部マッチングは最小費用流で求められる．

http://judge.u-aizu.ac.jp/onlinejudge/review.jsp?rid=3952428#1

Educational Codeforces Round 29 F. Almost Permutation

概要

$n$ 要素の配列 $A\ (1 \leq a_i \geq n)$ について $q$ 個の情報が与えられる

$x \in [l_i,r_i$ ] について $a_x \geq v_i$
$x \in [l_i,r_i$ ] について $a_x \leq v_i$

配列で $i$ が存在する数を $\text{cnt}(i)$ とする． $q$ 個の情報に矛盾せずに $\sum_{i=1}^n \text{cnt}(i)$ を最小化しろ．ありえない場合は-1を出力せよ．

解法

始点 → 配列の $n$ 要素に対応する $n$ 頂点 → $1 \sim n$ の値に対応する $n$ 頂点 → 終点と並べたグラフを用意する．
「始点 → 配列の $n$ 要素に対応する $n$ 頂点」の辺は容量1，コスト0とする．
「配列の $n$ 要素に対応する $n$ 頂点 → $1 \sim n$ の値に対応する $n$ 頂点」の辺は配列の $i$ 番目が取りうる値の範囲に応じて，容量1コスト0 の辺を張る．
「 $1 \sim n$ の値に対応する $n$ 頂点 → 終点」の辺を使って $\sum_{i=1}^n \text{cnt}(i)$ を表現する． $a^2 - (a-1)^2 = 2a-1$ なので $b^2 = \sum_{i=1}^n 2i-1$ である．よって，容量が1でコストが $1,3,5,7,\ldots$ であるような辺を張ればよい．
このグラフで流量 $N$ の最小費用流を求めれば良い．

http://codeforces.com/contest/863/submission/63642531